练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在四棱锥P-ABCD，四边形ABCD是边长为3的正方形，平面平面，于点O，，点E在棱PB上，.

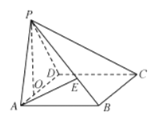
    （1）当时，求直线AE与平面PCD所成角的正弦值；

    （2）若二面角B-PC-D的余弦值为，求PO的长.

    【答案】（1）；（2）1.

    【解析】

    （1）先证明平面，然后以OP为z轴，建立空间直角坐标系Oxyz，算出和平面PCD的法向量的坐标即可

    （2）设，分别算出平面PCD和平面BPC的法向量即可.

    （1）平面平面，，平面平面

    平面

    平面.

    以OP为z轴，建立空间直角坐标系Oxyz，

    则，，，，，

    ，，.

    设平面PCD的法向量，

    即取.

    设直线AE与平面PCD所成角为，则，

    直线AE与平面PCD所成角的正弦值为.

    （2）设，则，，，

    ，.

    设平面PCD法向量，则

    取，同理可得平面BPC法向量，

    .

    ，解得.

    当二面角B─PC─D的余弦值为时，.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中．

    （I）求的单调区间；

    （Ⅱ）若R上有两个不同的零点，且，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x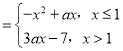），若存在x1，x2∈R且x1≠x2，使得f（x1）＝f（x2）成立，则实数a的取值范围是（ ）

    A.[3，+∞）B.（3，+∞）C.（﹣∞，3）D.（﹣∞，3]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝x2+acosx．

    （1）求函数f（x）的奇偶性．并证明当|a|≤2时函数f（x）只有一个极值点；

    （2）当a＝π时，求f（x）的最小值；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】把4个相同的小球全部放入2个不同的盒子里，每个盒子至少放1个球，不同的放法数记为；把4个不同的小球全部放入2个不同的盒子里，每个盒子至少放1个球，不同的放法数记为.现在从到的所有整数中（包括和两个整数）抽取3个数，则这3个数之和共有（ ）种结果.

    A.26B.27C.28D.29

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂根据市场需求开发三角花篮支架（如图），上面为花篮，支架由三根细钢管组成，考虑到钢管的受力和花篮质量等因素，设计支架应满足：①三根细钢管长均为1米（粗细忽略不计），且与地面所成的角均为；②架面与架底平行，且架面三角形与架底三角形均为等边三角形；③三根细钢管相交处的节点分三根细钢管上、下两段之比均为.定义：架面与架底的距离为“支架高度”，架底三角形的面积与“支架高度”的乘积为“支架需要空间”.

    （1）当时，求“支架高度”；

    （2）求“支架需要空间”的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在抗击新冠肺炎疫情期间，很多人积极参与了疫情防控的志愿者活动.各社区志愿者服务类型有：现场值班值守，社区消毒，远程教育宣传，心理咨询（每个志愿者仅参与一类服务）.参与A，B，C三个社区的志愿者服务情况如下表：

    社区

    社区服务总人数

    服务类型

    现场值班值守

    社区消毒

    远程教育宣传

    心理咨询

    A

    100

    30

    30

    20

    20

    B

    120

    40

    35

    20

    25

    C

    150

    50

    40

    30

    30

    （1）从上表三个社区的志愿者中任取1人，求此人来自于A社区，并且参与社区消毒工作的概率；

    （2）从上表三个社区的志愿者中各任取1人调查情况，以X表示负责现场值班值守的人数，求X的分布列；

    （3）已知A社区心理咨询满意率为0.85，B社区心理咨询满意率为0.95，C社区心理咨询满意率为0.9，“，，”分别表示A，B，C社区的人们对心理咨询满意，“，，”分别表示A，B，C社区的人们对心理咨询不满意，写出方差，，的大小关系.（只需写出结论）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

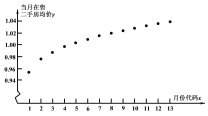
    【题目】某市房管局为了了解该市市民2018年1月至2019年1月期间购买二手房情况，首先随机抽样其中200名购房者，并对其购房面积（单位：万元/平方米，进行了一次调查统计，制成了如图1所示的频率分布直方图，接着调查了该市2018年1月至2019年1月期间当月在售二手房均价（单位：万元平方米），制成了如图2所示的散点图（图中月份代码1-13分别对应2018年1月至2019年1月）.

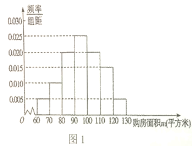
    （1）试估计该市市民的平均购房面积.

    （2）现采用分层抽样的方法从购房面积位于的40位市民中随机取4人，再从这4人中随机抽取2人，求这2人的购房面积恰好有一人在的概率.

    （3）根据散点图选和两个模型进行拟合，经过数据处理得到两个回归方程，分别为和，并得到一些统计量的值，如下表所示：

    0.000591

    0.000164

    0.00050

    请利用相关指数判断哪个模型的拟合效果更好，并用拟合效果更好的模型预测2019年6月份的二手房购房均价（精确到0.001）./span>

    参考数据：，，，，，，，，

    参考公式：.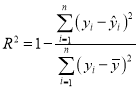

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某科研团队研发了一款快速检测某种疾病的试剂盒.为了解该试剂盒检测的准确性，质检部门从某地区（人数众多）随机选取了位患者和位非患者，用该试剂盒分别对他们进行检测，结果如下：

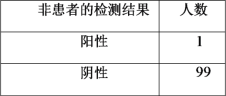
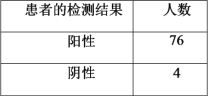
    （1）从该地区患者中随机选取一人，对其检测一次，估计此患者检测结果为阳性的概率；

    （2）从该地区患者中随机选取人，各检测一次，假设每位患者的检测结果相互独立，以表示检测结果为阳性的患者人数，利用（1）中所得概率，求的分布列和数学期望；

    （3）假设该地区有万人，患病率为.从该地区随机选取一人，用该试剂盒对其检测一次.若检测结果为阳性，能否判断此人患该疾病的概率超过？并说明理由.

    查看答案和解析>>

    同步练习册答案