
【题目】已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
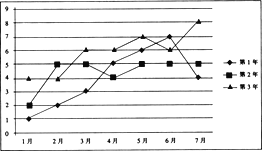
(1)试问这3年的前7个月中哪个月的月平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: 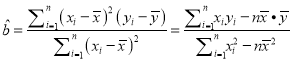 ,
, ![]() .
.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣ ![]() x3+bx2+cx+bc.
x3+bx2+cx+bc.
(1)若函数f(x)在x=1处有极值﹣ ![]() ,试确定b、c的值;
,试确定b、c的值;
(2)若b=1,f(x)存在单调递增区间,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kx2+(3+k)x+3,其中k为常数,且k≠0.
(1)若f(2)=3,求函数f(x)的表达式;
(2)在(1)的条件下,设函数g(x)=f(x)﹣mx,若g(x)在区间[﹣2,2]上是单调函数,求实数m的取值范围;
(3)是否存在k使得函数f(x)在[﹣1,4]上的最大值是4?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lnx+ax2﹣ax+5,a∈R.
(1)若函数f(x)在x=1处有极值,求实数a的值;
(2)若函数f(x)在区间(0,+∞)内单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高二年级共有1600人,现统计他们某项任务完成时间介于30分钟到90分钟之间,图中是统计结果的频率分布直方图.

(1)求平均值、众数、中位数;
(2)若学校规定完成时间在![]() 分钟内的成绩为
分钟内的成绩为![]() 等;完成时间在
等;完成时间在![]() 分钟内的成绩为
分钟内的成绩为![]() 等;完成时间在
等;完成时间在![]() 分钟内的成绩为
分钟内的成绩为![]() 等,按成绩分层抽样从全校学生中抽取10名学生,则成绩为
等,按成绩分层抽样从全校学生中抽取10名学生,则成绩为![]() 等的学生抽取人数为?
等的学生抽取人数为?
(3)在(2)条件下抽取的成绩为![]() 等的学生中再随机选取两人,求两人中至少有一人完成任务时间在
等的学生中再随机选取两人,求两人中至少有一人完成任务时间在![]() 分钟的概率.
分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对具有线性相关关系的两个变量y与x进行回归分析,得到一组样本数据(x1 , y1),(x2 , y2)…(xn , yn),则下列说法中不正确的是( )
A.若最小二乘法原理下得到的回归直线方程 ![]() =0.52x+
=0.52x+ ![]() ,则y与x具有正相关关系
,则y与x具有正相关关系
B.残差平方和越小的模型,拟合的效果越好
C.在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适
D.用相关指数R2来刻画回归效果,R2越小说明拟合效果越好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合U={x∈N|0<x≤8},S={1,2,4,5},T={3,5,7},则S∩(CUT)=( )
A.{1,2,4}
B.{1,2,3,4,5,7}
C.{1,2}
D.{1,2,4,5,6,8}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com