
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
科目:高中数学 来源: 题型:选择题
 结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为$\frac{1}{2}$的小正方体堆积成的正方体).其中实圆•代表钠原子,空间圆?代表氯原子.建立空间直角坐标系Oxyz后,图中最上层中间的钠原子所在位置的坐标是( )
结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为$\frac{1}{2}$的小正方体堆积成的正方体).其中实圆•代表钠原子,空间圆?代表氯原子.建立空间直角坐标系Oxyz后,图中最上层中间的钠原子所在位置的坐标是( )| A. | ($\frac{1}{2}$,$\frac{1}{2}$,1) | B. | (0,0,1) | C. | (1,$\frac{1}{2}$,1) | D. | (1,$\frac{1}{2}$,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
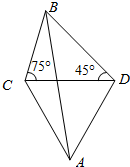 如图,某炮兵阵地位于A点,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC=$\sqrt{3}$ km,当目标出现在B点时,测得∠BCD=75°,∠CDB=45°,求炮兵阵地与目标的距离.
如图,某炮兵阵地位于A点,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC=$\sqrt{3}$ km,当目标出现在B点时,测得∠BCD=75°,∠CDB=45°,求炮兵阵地与目标的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知f(x)是定义在R上的偶函数,当0≤x<3时,y=x;当x≥3时,$y=-\frac{1}{3}{(x-3)^2}+3$
已知f(x)是定义在R上的偶函数,当0≤x<3时,y=x;当x≥3时,$y=-\frac{1}{3}{(x-3)^2}+3$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,f(x)≠0且g(x)≠0 | B. | ?x∈R,f(x)≠0或g(x)≠0 | ||
| C. | ?x0∈R,f(x0)≠0且g(x0)≠0 | D. | ?x0∈R,f(x0)≠0或g(x0)≠0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com