
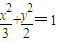 交于P(x1,y1),Q(x2,y2)两不同点,且△OPQ的面积S△OPQ=
交于P(x1,y1),Q(x2,y2)两不同点,且△OPQ的面积S△OPQ=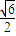 ,其中O为坐标原点.
,其中O为坐标原点.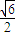 ?若存在,判断△DEG的形状;若不存在,请说明理由.
?若存在,判断△DEG的形状;若不存在,请说明理由.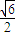
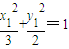 ①
①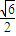 ,
,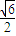 ②
②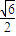 ,|y1|=1.此时x12+x22=3,y12+y22=2;
,|y1|=1.此时x12+x22=3,y12+y22=2;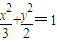 得
得 ,x1•x2=
,x1•x2=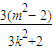 ,
, =
=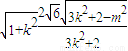 ,
,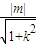 ,
,

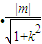 =
=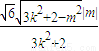 ,
,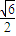 ,
,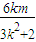 )2-2
)2-2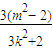 =3,
=3, (3-x12)+
(3-x12)+ (3-x22)=4-
(3-x22)=4- (x12+x22)=2;
(x12+x22)=2;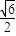 ,|PQ|=2|y1|=2,
,|PQ|=2|y1|=2,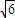 .
.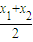 =-
=-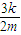 ,
,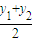 =k
=k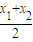 +m=
+m=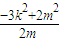 =
=
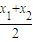 )2+(
)2+(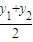 )2=
)2=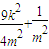 =
=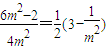 ,
,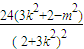 =
=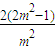 =2(2+
=2(2+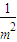 ),
),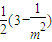 ×
× =(3-
=(3-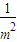 )(2+
)(2+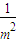 )
)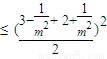 =
= .
.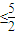 .当且仅当
.当且仅当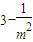 =2+
=2+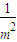 ,
,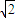 时,等号成立.
时,等号成立. ;
;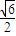 ,
,
 ;v2=y12=y22=1.
;v2=y12=y22=1.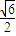 中选取,
中选取,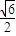 ,±1)这四点中选取三个不同点,
,±1)这四点中选取三个不同点,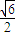 矛盾.
矛盾.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
| 8 |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
| 8 |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 3 |
| y2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012年吉林省高考数学仿真模拟试卷3(理科)(解析版) 题型:解答题
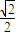 的椭圆C:
的椭圆C: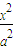 +
+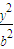 =1(a>b>0)过点M(
=1(a>b>0)过点M(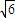 ,1),O为坐标原点.
,1),O为坐标原点. 的一条切线,试证明∠AOB=
的一条切线,试证明∠AOB=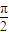 .它的逆命题成立吗?若成立,请给出证明;否则,请说明理由.
.它的逆命题成立吗?若成立,请给出证明;否则,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com