
【题目】设函数![]() ,则下列命题中正确的个数是( )
,则下列命题中正确的个数是( )
①当![]() 时,函数
时,函数![]() 在
在![]() 上是单调增函数;
上是单调增函数;
②当![]() 时,函数
时,函数![]() 在
在![]() 上有最小值;
上有最小值;
③函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
④方程![]() 可能有三个实数根.
可能有三个实数根.
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
将![]() 转化为分段函数,进而分别判断.
转化为分段函数,进而分别判断.
![]() =
=![]() ,
,
当b>0时,结合一元二次方程根与系数的关系,可判断y=![]() ,在(-
,在(-![]() ,0 )上是增函数,y=
,0 )上是增函数,y=![]() ,在[0,+
,在[0,+![]() )上是增函数,且x=0时,函数图象连续,故f(x)在R上是单调增函数.故①正确;
)上是增函数,且x=0时,函数图象连续,故f(x)在R上是单调增函数.故①正确;
当b<0时,f(x)的值域是R,没有最小值,故②错误;
若f(x)=|x|x+bx,f(-x)=-f(x),故函数f(x)是奇函数,即函数f(x)的图象关于(0,0)对称.而函数f(x)=|x|x+bx+c的图象是由函数f(x)=|x|x+bx的图象向上(下)平移![]() 个单位 ,故图象一定是关于(0,c)对称的,故③正确;
个单位 ,故图象一定是关于(0,c)对称的,故③正确;
令b=-2,c=0,则f(x)=|x|x-2x=0,解得x=0,2,-2.所以④正确.
故选C.


科目:高中数学 来源: 题型:
【题目】设 ![]() 为椭圆
为椭圆 ![]() 上任一点,
上任一点,![]() ,
,![]() 为椭圆的焦点,
为椭圆的焦点,![]() ,离心率为
,离心率为 ![]() .
.
(1)求椭圆的标准方程;
(2)直线 ![]() 经过点
经过点 ![]() ,且与椭圆交于
,且与椭圆交于 ![]() ,
,![]() 两点,若直线
两点,若直线 ![]() ,
,![]() ,
,![]() 的斜率依次成等比数列,求直线
的斜率依次成等比数列,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方体![]() 的棱长为1,点
的棱长为1,点![]() 是棱
是棱![]() 上的动点,
上的动点,![]() 是棱
是棱![]() 上一点,
上一点,![]() .
.

(1)求证:![]() ;
;
(2)若直线![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并证明你的结论;
的位置,并证明你的结论;
(3)设点![]() 在正方体的上底面
在正方体的上底面![]() 上运动,求总能使
上运动,求总能使![]() 与
与![]() 垂直的点
垂直的点![]() 所形成的轨迹的长度.(直接写出答案)
所形成的轨迹的长度.(直接写出答案)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大西洋鲑鱼每年都要逆流而上,游回产地产卵,经研究发现鲑鱼的游速可以表示为函数y=![]() log3(
log3(![]() ),单位是m/s,θ是表示鱼的耗氧量的单位数.
),单位是m/s,θ是表示鱼的耗氧量的单位数.
(1)当一条鲑鱼的耗氧量是900个单位时,它的游速是多少?
(2)计算一条鱼静止时耗氧量的单位数。
(3)某条鲑鱼想把游速提高1 m/s,那么它的耗氧量的单位数是原来的多少倍?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,等腰![]() 的底边
的底边![]() ,高
,高![]() ,点
,点![]() 是线段
是线段![]() 上异于点
上异于点![]() 的动点,点
的动点,点![]() 在
在![]() 边上,且
边上,且![]() ,现沿
,现沿![]() 将△
将△![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() ,记
,记![]() ,
, ![]() 表示四棱锥
表示四棱锥![]() 的体积.
的体积.
(1)求![]() 的表达式;(2)当
的表达式;(2)当![]() 为何值时,
为何值时, ![]() 取得最大,并求最大值。
取得最大,并求最大值。
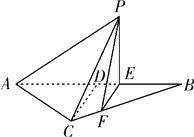
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位建造一间地面面积为12![]() 的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度![]() 不得超过
不得超过![]() 米,房屋正面的造价为400元/
米,房屋正面的造价为400元/![]() ,房屋侧面的造价为150元/
,房屋侧面的造价为150元/![]() ,屋顶和地面的造价费用合计为5800元,如果墙高为3
,屋顶和地面的造价费用合计为5800元,如果墙高为3![]() ,且不计房屋背面的费用.
,且不计房屋背面的费用.
(1)把房屋总价![]() 表示成
表示成![]() 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(2)当侧面的长度为多少时,总造价最低?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() >0,
>0, ![]() ≠1,
≠1, ![]() ≠﹣1),是定义在(﹣1,1)上的奇函数.
≠﹣1),是定义在(﹣1,1)上的奇函数.
(1)求实数![]() 的值;
的值;
(2)当![]() =1时,判断函数
=1时,判断函数![]() 在(﹣1,1)上的单调性,并给出证明;
在(﹣1,1)上的单调性,并给出证明;
(3)若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为![]() ,圆心角为
,圆心角为![]() 的扇形金属材料中剪出一个长方形
的扇形金属材料中剪出一个长方形![]() ,并且
,并且![]() 与
与![]() 的平分线
的平分线![]() 平行,设
平行,设![]() .
.

(1)试将长方形![]() 的面积
的面积![]() 表示为
表示为![]() 的函数;
的函数;
(2)若将长方形![]() 弯曲,使
弯曲,使![]() 和
和![]() 重合焊接制成圆柱的侧面,当圆柱侧面积最大时,求圆柱的体积(假设圆柱有上下底面);为了节省材料,想从△
重合焊接制成圆柱的侧面,当圆柱侧面积最大时,求圆柱的体积(假设圆柱有上下底面);为了节省材料,想从△![]() 中直接剪出一个圆面作为圆柱的一个底面,请问是否可行?并说明理由.
中直接剪出一个圆面作为圆柱的一个底面,请问是否可行?并说明理由.
(参考公式:圆柱体积公式![]() .其中
.其中![]() 是圆柱底面面积,
是圆柱底面面积,![]() 是圆柱的高;等边三角形内切圆半径
是圆柱的高;等边三角形内切圆半径![]() .其中
.其中![]() 是边长)
是边长)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com