
【题目】在四棱柱![]() 中,
中,![]() ,
,![]() 且
且![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
(1)证明:![]() .
.
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)根据三角形全等证明AC⊥BD,结合![]() 可得AC⊥平面
可得AC⊥平面![]() ,故而
,故而![]() ;(2)以
;(2)以![]() ,
,![]() 的交点
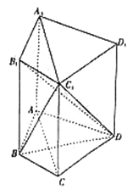
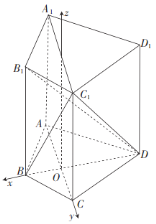
的交点![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,计算平面
,计算平面![]() 的法向量,利用线面角的向量公式求解即可
的法向量,利用线面角的向量公式求解即可
(1)证明:∵AD=CD,∴∠DAC=∠DCA,
又∠BAD=∠BCD,∴∠BAC=∠BCA,∴AB=AC,
∴△ABD≌△CBD,∴∠ADB=∠CDB,
∴△AOD≌△COD,∴∠AOD=∠COD=90°,
∴AC⊥BD,
又因为![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() 所以
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)以![]() ,
,![]() 的交点
的交点![]() 为原点,过O作平行于
为原点,过O作平行于![]() 的直线为z轴,建立如图所示的空间直角坐标系
的直线为z轴,建立如图所示的空间直角坐标系![]() ,由(1)及
,由(1)及![]() ,知
,知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由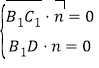 ,得
,得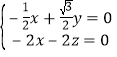 ,
,
所以![]() ,令
,令![]() ,得
,得![]() .
.
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则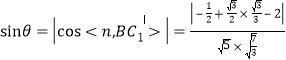
![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 是长轴的一个端点,弦
是长轴的一个端点,弦![]() 过椭圆的中心O,点C在第一象限,且
过椭圆的中心O,点C在第一象限,且![]() ,
,![]() .
.
(1)求椭圆的标准方程;
(2)设P、Q为椭圆上不重合的两点且异于A、B,若![]() 的平分线总是垂直于x轴,问是否存在实数
的平分线总是垂直于x轴,问是否存在实数![]() ,使得
,使得![]() ?若不存在,请说明理由;若存在,求
?若不存在,请说明理由;若存在,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
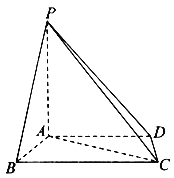
【题目】已知四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)当![]() 变化时,点
变化时,点![]() 到平面
到平面![]() 的距离是否为定值?若是,请求出该定值;若不是,请说明理由;
的距离是否为定值?若是,请求出该定值;若不是,请说明理由;
(2)当直线![]() 与平面
与平面![]() 所成的角为45°时,求二面角
所成的角为45°时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:对任意两个正整数
满足:对任意两个正整数![]()
![]() ,
,![]() 与
与![]() 至少有一个成立,则称这个数列为“和谐数列”.
至少有一个成立,则称这个数列为“和谐数列”.
(Ⅰ)求证:若数列![]() 为等差数列,则
为等差数列,则![]() 为“和谐数列”;
为“和谐数列”;
(Ⅱ)求证:若数列![]() 为“和谐数列”,则数列
为“和谐数列”,则数列![]() 从第
从第![]() 项起为等差数列;
项起为等差数列;
(Ⅲ)若![]() 是各项均为整数的“和谐数列”,满足
是各项均为整数的“和谐数列”,满足![]() ,且存在
,且存在![]() 使得
使得![]() ,
,![]() ,求p的所有可能值.
,求p的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十七世纪,法国数学家费马提出猜想;“当整数![]() 时,关于
时,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 没有正整数解”,经历三百多年,1995年英国数学家安德鲁
没有正整数解”,经历三百多年,1995年英国数学家安德鲁![]() 怀尔斯给出了证明,使它终成费马大定理,则下面命题正确的是( )
怀尔斯给出了证明,使它终成费马大定理,则下面命题正确的是( )
①对任意正整数![]() ,关于
,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 都没有正整数解;
都没有正整数解;
②当整数![]() 时,关于
时,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 至少存在一组正整数解;
至少存在一组正整数解;
③当正整数![]() 时,关于
时,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 至少存在一组正整数解;
至少存在一组正整数解;
④若关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 至少存在一组正整数解,则正整数
至少存在一组正整数解,则正整数![]() ;
;
A.①②/span>B.①③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年联想集团以28亿收购摩托罗拉移动公司,并计划投资30亿元来发展改品牌,2014年摩托罗拉手机的销售量为100万部,据专家预测,从2015年起,摩托罗拉手机的销售量每年比上上一年增加100万部,每年的销售利润比上一年减少10%,已知2014年销售利润平均每部为300元.
(1)若2014年看作第一年,第n年的销售利润为多少?
(2)到2020年年底,中国联想集团能否通过摩托罗拉手机实现盈利?(即销售利润超过总投资)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com