
【题目】已知二次函数f(x)=ax2+bx+c(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有f(x)≤![]() (x+2)2成立.
(x+2)2成立.
(1)证明:f(2)=2;
(2)若f(-2)=0,求f(x)的表达式;
【答案】(1)2(2)![]()
【解析】
(1)由f(x)≥x得f(2)≥2因为当x∈(1,3)时,有f(x)≤![]() 成立,所以f(2)≤
成立,所以f(2)≤![]() =2.从而求得f(2)的值即可;
=2.从而求得f(2)的值即可;
(2)由![]() 得出a,b,c的关系式,于是f(x)=ax2+
得出a,b,c的关系式,于是f(x)=ax2+![]() x+1﹣4a,结合f(x)≥xax2﹣
x+1﹣4a,结合f(x)≥xax2﹣![]() x+1﹣4a≥0.结合方程的思想求得a值即可得出f(x)的表达式.
x+1﹣4a≥0.结合方程的思想求得a值即可得出f(x)的表达式.
证明:(1)由f(x)≥x得f(2)≥2.
因为当x∈(1,3)时,有f(x)≤![]() 成立,所以f(2)≤
成立,所以f(2)≤![]() =2.
=2.
所以f(2)=2.
解:(2)由![]() 得
得![]()
从而有b=![]() ,c=1﹣4a.于是f(x)=ax2+
,c=1﹣4a.于是f(x)=ax2+![]() x+1﹣4a.
x+1﹣4a.
f(x)≥xax2﹣![]() x+1﹣4a≥0.
x+1﹣4a≥0.
若a=0,则﹣![]() x+1≥0不恒成立.
x+1≥0不恒成立.
所以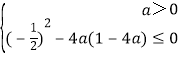 即
即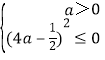 解得a=
解得a=![]() .
.
当a=![]() 时,f(x)=
时,f(x)=![]()
满足f(x)≤![]() .
.
故f(x)=![]() .
.


科目:高中数学 来源: 题型:
【题目】有如下几个结论: ①相关指数R2越大,说明残差平方和越小,模型的拟合效果越好; ②回归直线方程:![]() ,一定过样本点的中心:
,一定过样本点的中心:![]() ③残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适; ④在独立性检验中,若公式
③残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适; ④在独立性检验中,若公式![]() ,中的|ad-bc|的值越大,说明“两个分类变量有关系”的可能性越强.其中正确结论的个数有( )个.
,中的|ad-bc|的值越大,说明“两个分类变量有关系”的可能性越强.其中正确结论的个数有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面的折线图表示某商场一年中各月份的收入、支出情况,据此判断下列说法错误的是( )

A. 2至3月份的收入的变化率与11至12月份的收入的变化率相同
B. 支出最高值与支出最低值的比是6:1
C. 第三季度的月平均收入为50万元
D. 利润最高的月份是2月份(利润=收入-支出)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sin2x的图象先向左平移 ![]() 个单位长度,然后将所有点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应函数解析式为( )
个单位长度,然后将所有点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应函数解析式为( )
A.![]()
B.y=2cos2x
C.y=2sin2x
D.y=cosx
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在矩形ABCD中,已知AB=3AD,E,F为AB的两个三等分点,AC,DF交于点G.
(1)证明:EG![]() DF;
DF;
(2)设点E关于直线AC的对称点为![]() ,问点
,问点![]() 是否在直线DF上,并说明理由.
是否在直线DF上,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若在区间
,若在区间![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交警部门从某市参加![]() 年汽车驾照理论考试的
年汽车驾照理论考试的![]() 名学员中用系统抽样的方法抽出
名学员中用系统抽样的方法抽出![]() 名学员,将其成绩(均为整数)分成四段
名学员,将其成绩(均为整数)分成四段![]() ,
,![]() ,
,![]() ,
,![]() 后画出的频率分布直方图如图所示,回答下列问题:
后画出的频率分布直方图如图所示,回答下列问题:

(1)求图中![]() 的值;
的值;
(2)估计该市![]() 年汽车驾照理论考试及格的人数(不低于
年汽车驾照理论考试及格的人数(不低于![]() 分为及格)及抽样学员成绩的平均数;
分为及格)及抽样学员成绩的平均数;
(3)从第一组和第二组的样本中任意选出![]() 名学员,求
名学员,求![]() 名学员均为第一组学员的概率.
名学员均为第一组学员的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=a|x﹣b|+c满足①函数f(x)的图象关于x=1对称;②在R上有大于零的最大值;③函数f(x)的图象过点(0,1);④a,b,c∈Z,试写出一组符合要求的a,b,c的值 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com