
【题目】已知F1 , F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A,B两点,若△ABF2是正三角形,则这个椭圆的离心率是 .
【答案】![]()
【解析】解:∵△ABF2是正三角形, ∴∠AF2B=60°,
∵直线AB与椭圆长轴垂直,
∴F2F1是正三角形△ABF2的高,∠AF2F1= ![]() ×60°=30°,
×60°=30°,
Rt△AF2F1中,设|AF1|=m,sin30°= ![]() ,
,
∴|AF2|=2m,|F1F2|= ![]()
因此,椭圆的长轴2a=|AF1|+|AF2|=3m,焦距2c= ![]() m
m
∴椭圆的离心率为e= ![]() =
= ![]() .
.
故答案为: ![]()

根据△ABF2是正三角形,且直线AB与椭圆长轴垂直,得到F2F1是正三角形△ABF2的高,∠AF2F1=30°.在Rt△AF2F1中,设|AF1|=m,可得 ![]() ,所以|AF2|=2m,用勾股定理算出|F1F2|=
,所以|AF2|=2m,用勾股定理算出|F1F2|= ![]() m,得到椭圆的长轴2a=|AF1|+|AF2|=3m,焦距2c=
m,得到椭圆的长轴2a=|AF1|+|AF2|=3m,焦距2c= ![]() m,所以椭圆的离心率为e=
m,所以椭圆的离心率为e= ![]() =
= ![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,设F1、F2分别为椭圆的左、右焦点,椭圆上任意一个动点M到左焦点F1的距离的最大值 为
,设F1、F2分别为椭圆的左、右焦点,椭圆上任意一个动点M到左焦点F1的距离的最大值 为 ![]() +1 (Ⅰ)求椭圆C的方程;
+1 (Ⅰ)求椭圆C的方程;
(Ⅱ)设直线L的斜率为k,且过左焦点F1 , 与椭圆C相交于P、Q两点,若△PQF2的面积为 ![]() ,试求k的值及直线L的方程.
,试求k的值及直线L的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若采用随机模拟的方法估计某运动员射击击中目标的概率.先由计算器给出0到9之间取整数的随机数,指定0,1,2,3表示没有击中目标,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组如下的随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该运动员射击4次至少击中3次的概率为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是奇函数,且定义域为(﹣∞,0)∪(0,+∞).若x<0时,f(x)=﹣x﹣1.
(1)求f(x)的解析式;
(2)解关于x的不等式f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意实数a,b,c,d,以下四个命题中的真命题是( )
A.若a>b,c≠0则ac>bc
B.若a>b>o,c>d则ac>bd
C.若a>b,则 ![]()
D.若ac2>bc2则a>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几年来,网上购物风靡,快递业迅猛发展,某市的快递业务主要由两家快递公司承接,即圆通公司与申通公司:“快递员”的工资是“底薪+送件提成”:这两家公司对“快递员”的日工资方案为:圆通公司规定快递员每天底薪为70元,每送件一次提成1元;申通公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成10元,假设同一公司的快递员每天送件数相同,现从这两家公司各随机抽取一名快递员并记录其100天的送件数,得到如下条形图:
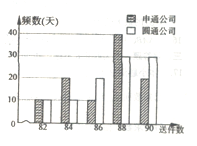
(1)求申通公司的快递员一日工资![]() (单位:元)与送件数
(单位:元)与送件数![]() 的函数关系;
的函数关系;
(2)若将频率视为概率,回答下列问题:
①记圆通公司的“快递员”日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小王想到这两家公司中的一家应聘“快递员”的工作,如果仅从日收入的角度考虑,请你利用所学过的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣1.
(1)求f(3)+f(﹣1);
(2)求f(x)在R上的解析式;
(3)求不等式﹣7≤f(x)≤3的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数F(x)=g(x)+h(x)=ex , 且g(x),h(x)分别是R上的偶函数和奇函数,若对任意的x∈(0,+∞),不等式g(2x)≥ah(x)恒成立,则实数a的取值范围是( )
A.(﹣∞,2 ![]() ]
]
B.(﹣∞,2 ![]() )
)
C.(﹣∞,2]
D.(﹣∞,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com