
【题目】2018年9~12月某市邮政快递业务量完成件数较2017年9~12月同比增长25%,该市2017年9~12月邮政快递业务量柱形图及2018年9~12月邮政快递业务量结构扇形图如图所示,根据统计图,给出下列结论:
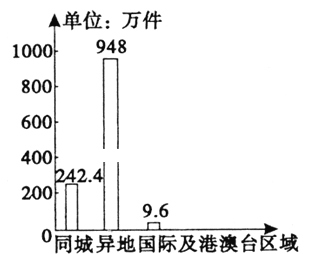
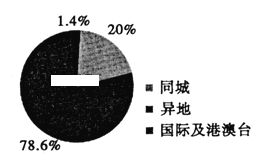
①2018年9~12月,该市邮政快递业务量完成件数约1500万件;
②2018年9~12月,该市邮政快递同城业务量完成件数与2017年9~12月相比有所减少;
③2018年9~12月,该市邮政快递国际及港澳台业务量同比增长超过75%,其中正确结论的个数为( )
A. 3
B. 2
C. 1
D. 0
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】定义:如果数列![]() 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称![]() 为“三角形”数列,对于“三角形”数列
为“三角形”数列,对于“三角形”数列![]() ,如果函数
,如果函数![]() 使得
使得![]() 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称![]() 是数列
是数列![]() 的“保三角形函数”
的“保三角形函数”![]() .
.
(1)已知![]() 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若![]() 是数列
是数列![]() 的“保三角形函数”,求k的取值范围;
的“保三角形函数”,求k的取值范围;
(2)已知数列![]() 的首项为2010,
的首项为2010,![]() 是数列
是数列![]() 的前n项和,且满足
的前n项和,且满足![]() ,证明
,证明![]() 是“三角形”数列.
是“三角形”数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是直角坐标平面内y轴及y轴的右侧的动点,点
是直角坐标平面内y轴及y轴的右侧的动点,点![]() 到直线
到直线![]() (
(![]() 是正常数)的距离为
是正常数)的距离为![]() ,到点
,到点![]() 的距离为
的距离为![]() ,且
,且![]() .
.
(1)求动点![]() 所在曲线
所在曲线![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 交于不同两点
交于不同两点![]() ,分别过点
,分别过点![]() 作直线
作直线![]() 的垂线,对应的垂足分别为
的垂线,对应的垂足分别为![]() ,记
,记![]() (
(![]() 是(2)中的点),
是(2)中的点),![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】费马点是指三角形内到三角形三个顶点距离之和最小的点。当三角形三个内角均小于![]() 时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等均为
时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等均为![]() 。根据以上性质,函数
。根据以上性质,函数![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,AB=1,BC=2,AC![]() ,PC
,PC![]() ,PA
,PA![]() ,PB
,PB![]() ,E是线段BC的中点.
,E是线段BC的中点.
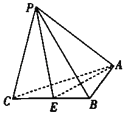
(1)求点C到平面APE的距离d;
(2)求二面角P﹣EA﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() ,点
,点![]() 在二次函数
在二次函数![]() 的图象上.
的图象上.
(1)试判断数列![]() 是否为算术平方根递推数列?若是,请说明你的理由;
是否为算术平方根递推数列?若是,请说明你的理由;
(2)记![]() ,求证:数列
,求证:数列![]() 是等比数列,并求出通项公式
是等比数列,并求出通项公式![]() ;
;
(3)在数列![]() 中依据某种顺序从左至右取出其中的项
中依据某种顺序从左至右取出其中的项![]() ,…,把这些项重新组成一个新数列
,…,把这些项重新组成一个新数列![]() ,….若数列
,….若数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的无穷等比数列,且数列
的无穷等比数列,且数列![]() 各项的和为
各项的和为![]() ,求正整数
,求正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
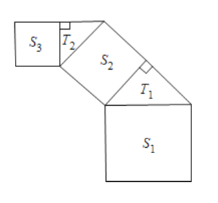
【题目】如图所示,正方形上连接等腰直角三角形,直角三角形上再连接正方形……如此无限重复下去,设正方形面积为![]() ,三角形面积为
,三角形面积为![]() .当第一个正方形的边长为2时,则这些正方形和三角形的面积的总和为______.
.当第一个正方形的边长为2时,则这些正方形和三角形的面积的总和为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位从一所学校招收某类特殊人才.对![]() 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
| 一般 | 良好 | 优秀 |
一般 |
|
|
|
良好 |
|
|
|
优秀 |
|
|
|
例如表中运动协调能力良好且逻辑思维能力一般的学生是![]() 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这![]() 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)从运动协调能力为优秀的学生中任意抽取![]() 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com