
【题目】设函数![]() .
.
(1) 解不等式![]() ;
;
(2) 设函数![]() ,若函数
,若函数![]() 为偶函数,求实数
为偶函数,求实数![]() 的值;
的值;
(3) 当![]() 时,是否存在实数
时,是否存在实数![]() (其中
(其中![]() ),使得不等式
),使得不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
【题目】(本题满分12分)如下图所示:在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
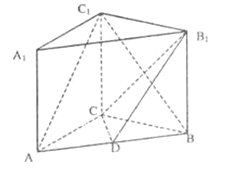
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求证:AC1∥平面CDB1;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某校高二学生的身高是否与性别有关,随机调查该校64名高二学生,得到2×2列联表如表:
男生 | 女生 | 总计 | |
身高低于170cm | 8 | 24 | 32 |
身高不低于170cm | 26 | 6 | 32 |
总计 | 34 | 30 | 64 |
附:K2![]()
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
由此得出的正确结论是( )
A.在犯错误的概率不超过0.01的前提下,认为“身高与性别无关”
B.在犯错误的概率不超过0.01的前提下,认为“身高与性别有关”
C.有99.9%的把握认为“身高与性别无关”
D.有99.9%的把握认为“身高与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 个孩子在黄老师的后院玩球,突然传来一阵打碎玻璃的响声,黄老师跑去察看,发现一扇窗户玻璃被打破了,老师问:“谁打破的?”宝宝说:“是可可打破的.”可可说:“是毛毛打破的.”毛毛说:“可可说谎.”多多说:“我没有打破窗子.”如果只有一个小孩说的是实话,那么打碎玻璃的是( )
个孩子在黄老师的后院玩球,突然传来一阵打碎玻璃的响声,黄老师跑去察看,发现一扇窗户玻璃被打破了,老师问:“谁打破的?”宝宝说:“是可可打破的.”可可说:“是毛毛打破的.”毛毛说:“可可说谎.”多多说:“我没有打破窗子.”如果只有一个小孩说的是实话,那么打碎玻璃的是( )
A.宝宝B.可可C.多多D.毛毛
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 均为假命题;②命题“若
均为假命题;②命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”; ③“
”; ③“![]() ,则
,则![]() ”的否定是“
”的否定是“![]() ,则
,则![]() ”;④在
”;④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件.其中正确的命题的个数是( )
”的充要条件.其中正确的命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列三个命题:
①函数![]() 的单调增区间是
的单调增区间是![]()
②经过任意两点的直线,都可以用方程![]() 来表示;
来表示;
③命题![]() :“
:“![]()
![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”,
”,
其中正确命题的个数有( )个
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com