Question

【题目】如图示，A，B分别是椭圆C： （a＞b＞0）的左右顶点，F为其右焦点，2是|AF与|FB|的等差中项， 是|AF|与|FB|的等比中项．点P是椭圆C上异于A、B的任一动点，过点A作直线l⊥x轴．以线段AF为直径的圆交直线AP于点A，M，连接FM交直线l于点Q．

（1）求椭圆C的方程；
（2）试问在x轴上是否存在一个定点N，使得直线PQ必过该定点N？若存在，求出N点的坐标，若不存在，说明理由．

Answer 1

【答案】
（1）

解：由题意得|AF|=a+c，|FB|=a﹣c，

即 ，

解得：a=2，c=1，

∴b2=4﹣1=3，

∴所求椭圆的方程为： =1

（2）

解：假设在x轴上存在一个定点N（n，0），使得直线PD必过定点N（n，0），

设动点P（x0，y0），由于P点异于A，B，

故y0≠0，且x0≠±2，

由点P在椭圆上，

故有 ，∴ ，①

又由（1）知A（﹣2，0），F（1，0），∴直线AP的斜率 ，

又点M是以线段AF为直径的圆与直线AP的交点，∴AP⊥FM，

∴ ，

∴直线FM的方程：

联立FM，l的方程 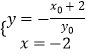，得交点Q（﹣2， ）．

∴P、Q两点连线的斜率 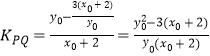，②

将①式代入②式，并整理得：kPQ= ，

又P，N两点连线的斜率 ，

若直线QP必过定点N（n，0），则必有kPQ=KPN恒成立

即 整理得： ，③

将①式代入③式，得

解得：n=2，

故直线x过定点（2，0）．

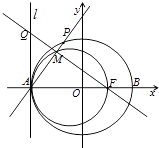
【解析】（1）由题意得|AF|=a+c，|FB|=a﹣c，再由2是|AF与|FB|的等差中项， 是|AF|与|FB|的等比中项，能求出椭圆的方程．（2）假设在x轴上存在一个定点N（n，0），使得直线PD必过定点N（n，0），设动点P（x0 ， y0），由点P在椭圆上，求出 ，再求出直线FM的方程，联立FM，l的方程，得交点Q，由此能求出直线x过定点（2，0）．