Question

【题目】如图，在梯形中，，，，四边形是直角梯形，，，，平面平面.

（1）求证：平面；

（2）在线段上是否存在一点，使得平面与平面所成的锐二面角的余弦值为，若存在，求出点的位置；若不存在，说明理由.

Answer 1

【答案】（1）见解析；（2）为线段的中点.

【解析】

（1）由余弦定理，结合勾股定理可证明，再利用面面垂直的性质定理可得结论；（2）先证明，以为原点，分别以，，所在直线为轴、轴、轴建立空间直角坐标系，设，取平面的一个法向量为，利用向量垂直数量积为零求出平面的一个法向量，利用空间向量夹角余弦公式求得,从而可得结果.

（1）在梯形中，， ， ，

， ，

，，

平面平面，平面平面，

平面.

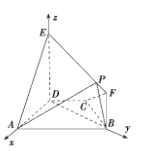
（2）平面，.如图，以为原点，分别以，，所在直线为轴、轴、轴建立空间直角坐标系，则，，，，，，，.设，

则，取平面的一个法向量为设平面的一个法向量为，

由，得，

令，得，，

为平面的一个法向量，

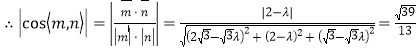，解得，

即当为线段的中点时满足题意.