
| |||||||||||||||
(1) |
方法一:解:记AC与BD的交点为O,连接OE, ∵O、M分别是AC、EF的中点,ACEF是矩形, ∴四边形AOEM是平行四边形,∴AM∥OE. ∵
方法二:建立如图所示的空间直角坐标系.
|
(2) |
方法一:在平面AFD中过A作AS⊥DF于S,连结BS, ∵AB⊥AF,AB⊥AD, ∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影, 由三垂线定理得BS⊥DF. ∴∠BSA是二面角A—DF—B的平面角. 在RtΔASB中, ∴二面角A—DF—B的大小为60o.
方法二:∵AF⊥AB,AB⊥AD,AF ∴ ∵ ∴
∴cos<
|
(3) |
方法一:解:设CP=t(0≤t≤2),作PQ⊥AB于Q,则PQ∥AD, ∵PQ⊥AB,PQ⊥AF, ∴PQ⊥平面ABF, 在RtΔPQF中,∠FPQ=60o,PF=2PQ. ∵△PAQ为等腰直角三角形,∴ ∴ 所以t=1或t=3(舍去)即点P是AC的中点. 方法二:设P(t,t,0)(0≤t≤
∴ |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.| 5 |
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
|
| x2 |
| 12 |
| y2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省高三第三次模拟考试数学(文) 题型:解答题
选答题(本小题满分10分)(请考生在第22、23、24三道题中任选一题做答,并用2B铅笔在答题卡上把所选题目的题号涂黑。注意所做题号必须与所涂题目的题号一致,并在答题卡指定区域答题。如果多做,则按所做的第一题计分。)
22.选修4-1:几何证明选讲
如图,已知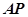 是⊙
是⊙ 的切线,
的切线,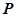 为切点,
为切点,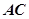 是⊙
是⊙ 的割线,与⊙
的割线,与⊙ 交于
交于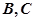 两点,圆心
两点,圆心 在
在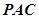 的内部,点
的内部,点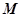 是
是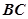 的中点。
的中点。
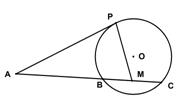
(1)证明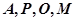 四点共圆;
四点共圆;
(2)求 的大小。
的大小。
23.选修4—4:坐标系与参数方程[来源:ZXXK]
已知直线 经过点
经过点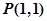 ,倾斜角
,倾斜角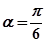 。
。
(1)写出直线 的参数方程;
的参数方程;
(2)设 与曲线
与曲线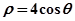 相交于两点
相交于两点 ,求点
,求点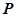 到
到 两点的距离之积。
两点的距离之积。
24.选修4—5:不等式证明选讲
若不等式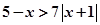 与不等式
与不等式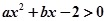 同解,而
同解,而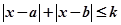 的解集为空集,求实数
的解集为空集,求实数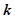 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2013年江苏省宿迁市高考数学一模试卷(解析版) 题型:解答题
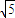 ,求线段AC的长度.
,求线段AC的长度. 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.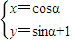 (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.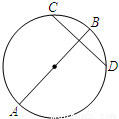
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com