
如图,已知正方形ABCD的边长为2,中心为O.设PA⊥平面ABCD,EC∥PA,且PA=2.

(1)当CE为多少时,PO⊥平面BED;
(2)在(Ⅰ)的情形下,求二面角E-PB-A的大小.
|
(1)当CE=1时,PO⊥平面BED. 证明如下:∵四边形ABCD为正方形,∴AC⊥BD. ∵PA⊥平面BD,∴AO为PO在平面BD上的射影,BD⊥PO. 过点E作EF∥AC,交PA于点F,连接OE,则 在△POE中, ∴PO⊥OE. ∵BD∩EO=O,∴PO⊥平面BED. (2)
如图,过E作EF⊥平面PAB于F,过F作FH⊥PB于H,连EH,则∠EHF为二面角F-PB-E的平面角.易证四边形ABRP为正方形,且F为RB的中点,∴FB=1,易得FH= 在Rt△EFH中, 因所求二面角为二面角F-PB-E的补角, 故所求的二面角的大小为 (向量方法略) |


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
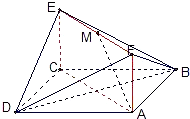 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=| 2 |
| 2 |
| ME |
| FM |
查看答案和解析>>
科目:高中数学 来源: 题型:
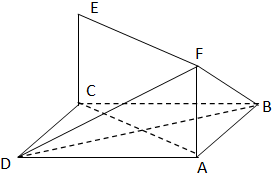 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.| 2 |
| 5 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com