Question

【题目】已知函数f（x）＝ax2－2x＋1.

（1）当,试讨论函数f（x）的单调性；

（2）若≤a≤1，且f（x）在[1,3]上的最大值为M（a），最小值为N（a），令g（a）＝M（a）－N（a），求g（a）的表达式；

（3）在（2）的条件下，求g（a）的最小值.

Answer 1

【答案】（1） 时增区间，减区间，时增区间，减区间

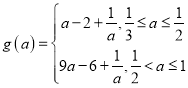（2） （3）

【解析】

试题分析：（1）通过讨论a的符合，结合二次函数的性质，从而判断出函数的单调性；（2）通过讨论a的范围，求出f（x）的单调区间，从而求出函数的最值，进而求出g（a）的解析式；（3）根据a的范围，求出g（a）的单调性，从而求出g（a）的最小值

试题解析：（1）

-----2分

（2）∵≤a≤1，∴f（x）的图象为开口向上的抛物线，且对称轴为x＝∈[1,3].

∴f（x）有最小值N（a）＝1－.

当2≤≤3时，a∈[，]，f（x）有最大值M（a）＝f（1）

＝a－1；

当1≤<2时，a∈（，1]，f（x）有最大值M（a）＝f（3）

＝9a－5；

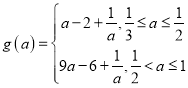∴ -----7分

（3）设≤a1<a2≤，则g（a1）－g（a2）＝（a1－a2）（1－）>0，

∴g（a1）>g（a2），∴g（a）在[，]上是减函数.

设<a1<a2≤1，则g（a1）－g（a2）＝（a1－a2）（9－）<0，∴g（a1）<g（a2），

∴g（a）在（，1]上是增函数.

∴当a＝时，g（a）有最小值. -----12分