
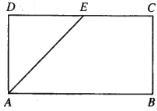
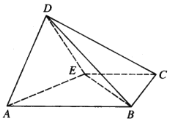
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.把
的中点.把![]() 沿
沿![]() 翻折,使得平面
翻折,使得平面![]() 平面
平面![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求![]() 所在直线与平面
所在直线与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)证明空间中两异面直线垂直的常用方法为先证明直线与平面垂直,再证明另一条直线在这个平面内;(Ⅱ)用等体积法求解,或建立空间直角坐标系,利用直线的方向向量和平面的法向量的夹角求解.
解:(Ⅰ)证明:∵![]() 为
为![]() 的中点,
的中点,
矩形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,则
,则![]() ,
,
∴![]() .
.
∵平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
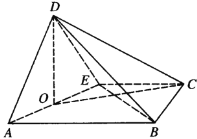
(Ⅱ)解法一:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() .
.
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,则
,则![]() ,
,
∴![]() ,则
,则![]() .
.
设![]() 所在直线与平面
所在直线与平面![]() 所成角为
所成角为![]() ,
,
∵![]() ,∴
,∴![]() ,
,
即![]() 所在直线与平面
所在直线与平面![]() 所成角的正弦值为
所成角的正弦值为![]()
解法二:取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
∴![]() 平面
平面![]() ,
,
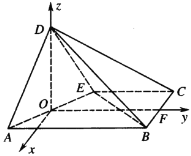
∴以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建
轴,建
立如图所示的空间直角坐标系.
则![]() ,
,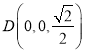 ,
,![]() ,
,![]() ,
,
∴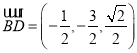 ,
,![]() ,
,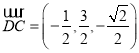 ,
,
∴设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
∴![]() ,
,![]() ,
,
所以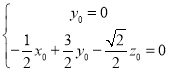 ,令
,令![]() ,则
,则![]()
∴![]() .
.
设![]() 所在直线与平面
所在直线与平面![]() 所成角为
所成角为![]() ,
,
∴![]() ,
,
即![]() 所在直线与平面
所在直线与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】天上有些恒星的亮度是会变化的,其中一种称为造父(型)变星,本身体积会膨胀收缩造成亮度周期性的变化.第一颗被描述的经典造父变星是在1784年.
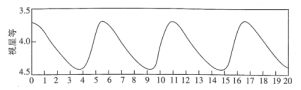
上图为一造父变星的亮度随时间的周期变化图,其中视星等的数值越小,亮度越高,则此变星亮度变化的周期、最亮时视星等,分别约是( )
A.5.5,3.7B.5.4,4.4C.6.5,3.7D.5.5,4.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校高三大理班周三上午四节、下午三节有六门科目可供安排,其中语文和数学各自都必须上两节而且两节连上,而英语、物理、化学、生物最多上一节,则不同的功课安排有________种情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将曲线方程![]() ,先向左平移2个单位,再向上平移2个单位,得到曲线C.
,先向左平移2个单位,再向上平移2个单位,得到曲线C.
(1)点M(x,y)为曲线C上任意一点,写出曲线C的参数方程,并求出![]() 的最大值;
的最大值;
(2)设直线l的参数方程为![]() ,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们称满足: ![]() (
(![]() )的数列
)的数列![]() 为“
为“![]() 级梦数列”.
级梦数列”.
(1)若![]() 是“
是“![]() 级梦数列”且
级梦数列”且![]() .求:
.求: ![]() 和
和![]() 的值;
的值;
(2)若![]() 是“
是“![]() 级梦数列”且满足
级梦数列”且满足![]() ,
, ![]() ,求
,求![]() 的最小值;
的最小值;
(3)若![]() 是“0级梦数列”且
是“0级梦数列”且![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() .证明:
.证明: ![]() (
(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
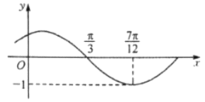
【题目】函数![]() 的图象如图所示,先将函数
的图象如图所示,先将函数![]() 图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移
图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,下列结论正确的是( )
的图象,下列结论正确的是( )
A.函数![]() 是奇函数B.函数
是奇函数B.函数![]() 在区间
在区间![]() 上是增函数
上是增函数
C.函数![]() 图象关于
图象关于![]() 对称D.函数
对称D.函数![]() 图象关于直线
图象关于直线![]() 对称
对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com