
【题目】如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且AB=1,BC=2, ∠ABC=60°,PA⊥平面ABCD,AE⊥PC于E,
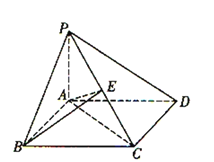
下列四个结论:①AB⊥AC;②AB⊥平面PAC;③PC⊥平面ABE;④BE⊥PC.正确的个数是( )
A.1B.2C.3D.4
科目:高中数学 来源: 题型:
【题目】直线l:ax+![]() y﹣1=0与x,y轴的交点分别为A,B,直线l与圆O:x2+y2=1的交点为C,D,给出下面三个结论:①a≥1,S△AOB=
y﹣1=0与x,y轴的交点分别为A,B,直线l与圆O:x2+y2=1的交点为C,D,给出下面三个结论:①a≥1,S△AOB=![]() ;②a≥1,|AB|<|CD|;③a≥1,S△COD<
;②a≥1,|AB|<|CD|;③a≥1,S△COD<![]() .其中,所有正确结论的序号是( )
.其中,所有正确结论的序号是( )
A.①②B.②③C.①③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,记集合
,记集合![]() .
.
(1)对于数列![]() ,写出集合
,写出集合![]() ;
;
(2)若![]() ,是否存在
,是否存在![]() ,使得
,使得![]() ?若存在,求出一组符合条件的
?若存在,求出一组符合条件的![]() ;若不存在,说明理由.
;若不存在,说明理由.
(3)若![]() ,把集合
,把集合![]() 中的元素从小到大排列,得到的新数列为
中的元素从小到大排列,得到的新数列为![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知对于任意![]() ,函数
,函数![]()
![]() 与
与![]()
![]() 的图像在
的图像在![]() 上都有三个不同交点.
上都有三个不同交点.
(1)写出![]() 的解析式,并求函数的最大值及此时的x的取值;
的解析式,并求函数的最大值及此时的x的取值;
(2)若函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,且
上单调递减,且![]() ,求
,求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环保部门要对所有的新车模型进行广泛测试,以确定它的行车里程的等级,下表是对100辆新车模型在一个耗油单位内行车里程(单位:公里)的测试结果.
分组 | 频数 |
| 6 |
| 10 |
| 20 |
| 30 |
| 18 |
| 12 |
| 4 |
(1)做出上述测试结果的频率分布直方图,并指出其中位数落在哪一组;
(2)用分层抽样的方法从行车里程在区间![]() 与
与![]() 的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在
的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
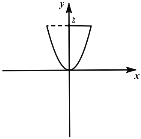
【题目】“辛卜生公式”给出了求几何体体积的一种计算方法:夹在两个平行平面之间的几何体,如果被平行于这两个平面的任何平面所截,截得的截面面积是截面高(不超过三次)的多项式函数,那么这个几何体的体积,就等于其上底面积、下底面积与四倍中截面面积的和乘以高的六分之一.即:![]() ,式中
,式中![]() ,
,![]() ,
,![]() ,
,![]() 依次为几何体的高,下底面积,上底面积,中截面面积.如图,现将曲线
依次为几何体的高,下底面积,上底面积,中截面面积.如图,现将曲线![]() 与直线
与直线![]() 及
及![]() 轴围成的封闭图形绕
轴围成的封闭图形绕![]() 轴旋转一周得到一个几何体.利用辛卜生公式可求得该几何体的体积
轴旋转一周得到一个几何体.利用辛卜生公式可求得该几何体的体积![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上的一点
上的一点![]() 到其左顶点
到其左顶点![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(
两点(![]() 与点
与点![]() 不重合),若以
不重合),若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,试证明:直线
,试证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 及
及![]() ;
;
(2)若![]() 且数列
且数列![]() 为周期函数,且最小正周期
为周期函数,且最小正周期![]() ,求
,求![]() 的值;
的值;
(3)是否存在![]() ,使得
,使得![]() 成等比数列?若存在,求出所有这样的
成等比数列?若存在,求出所有这样的![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,
,![]() 是圆M内一定点,动点P为圆M上任意一点,线段PN的垂直平分线l和半径MP相交于点C.
是圆M内一定点,动点P为圆M上任意一点,线段PN的垂直平分线l和半径MP相交于点C.
(1)求点C的轨迹方程;
(2)设直线![]() 与C交于不同两点A,B,点O为坐标原点,当
与C交于不同两点A,B,点O为坐标原点,当![]() 的面积S取最大值时,求
的面积S取最大值时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com