
【题目】已知函数![]() 。
。
(1)若f(x)的图象与g(x)的图象所在两条曲线的一个公共点在y轴上,且在该点处两条曲线的切线互相垂直,求b和c的值。
(2)若a=c=1,b=0,试比较f(x)与g(x)的大小,并说明理由;
(3)若b=c=0,证明:对任意给定的正数a,总存在正数m,使得当x![]() 时,
时,
恒有f(x)>g(x)成立。
【答案】(1)![]() (2)当
(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .(3)详见解析
.(3)详见解析
【解析】
试题分析:(1)由题意得![]() ,
,![]() ,即
,即![]() (2)构造函数
(2)构造函数![]() 则
则![]() .当
.当![]() 时,
时,![]() ,
,![]() ,
,![]()
当![]() 时,设
时,设![]() ,则
,则![]() ,当
,当![]() 时,
时, ![]() 取得极小值, 且极小值为
取得极小值, 且极小值为![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
,![]() (3)构造函数
(3)构造函数![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上有最小值,
上有最小值,![]() ,①若
,①若![]() ,存在
,存在![]() ,使当
,使当![]() 时,恒有
时,恒有![]() ;若
;若![]() ,存在
,存在![]() ,使当
,使当![]() 时,恒有
时,恒有![]() ;③若
;③若![]() ,存在
,存在![]() ,使当
,使当![]() 时,恒有
时,恒有![]() ;
;
试题解析:(1)解: ![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() 2分
2分
依题意:![]()
![]() ,所以
,所以![]()
![]() ; 4分
; 4分
(2)解: ![]() ,
,![]() 时,
时,![]() , 5分
, 5分
①![]() 时,
时,![]() ,
,![]() ,即
,即![]()
②![]() 时,
时,![]() ,
,![]() ,即
,即![]()
③![]() 时,令
时,令![]() ,则
,则![]() .
.
设![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增.
单调递增.
所以当![]() 时,
时, ![]() 取得极小值, 且极小值为
取得极小值, 且极小值为![]()
即![]() 恒成立,故
恒成立,故![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
因此,当![]() 时,
时, ![]() ,即
,即![]() . 9分
. 9分
综上,当![]() 时,
时,![]() ;当
;当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() . 10分
. 10分
![]() (3)
(3)
证法一:①若![]() ,由(2)知,当
,由(2)知,当![]() 时,
时, ![]() .即
.即![]() ,
,
所以,![]() 时,取
时,取![]() ,即有当
,即有当![]() ,恒有
,恒有![]() .
.
②若![]() ,
,![]() 即
即![]() ,等价于
,等价于![]() 即
即![]()
令![]() ,则
,则![]() .当
.当![]() 时,
时,![]()
![]() 内单调递增.
内单调递增.
取![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 内单调递增.
内单调递增.
又![]()
![]()
即存在![]() ,当
,当![]() 时,恒有
时,恒有![]() . 15分
. 15分
综上,对任意给定的正数![]() ,总存在正数
,总存在正数![]() ,使得当
,使得当![]() ,恒有
,恒有![]() . 16分
. 16分
证法二:设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调减,当
单调减,当![]() 时,
时,![]() ,
,![]() 单调增,
单调增,
故![]() 在
在![]() 上有最小值,
上有最小值,![]() , 12分
, 12分
①若![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
即当![]() 时,存在
时,存在![]() ,使当
,使当![]() 时,恒有
时,恒有![]() ;
;
②若![]() ,存在
,存在![]() ,使当
,使当![]() 时,恒有
时,恒有![]() ;
;
③若![]() ,同证明一的②, 15分
,同证明一的②, 15分
综上可得,对任意给定的正数![]() ,总存在
,总存在![]() ,当
,当![]() 时,恒有
时,恒有![]() . 16分
. 16分


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图.观察图形的信息,回答下列问题. 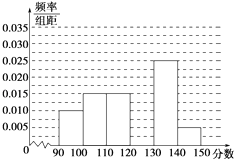
(1)从该校高三模拟考试的成绩中随机抽取一份,利用随机事件频率估计概率,求数学分数恰在[120,130)内的频率;
(2)估计本次考试的中位数;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( ) 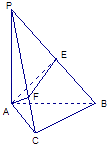
A.2
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B,C是椭圆M: ![]() 上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。

(1)求椭圆的离心率;
(2)若y轴被△ABC的外接圆所截得弦长为9,求椭圆方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设对于任意实数x,不等式|x+7|+|x﹣1|≥m恒成立.
(1)求m的取值范围;
(2)当m取最大值时,解关于x的不等式:|x﹣3|﹣2x≤2m﹣12.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{![]() }中,
}中,![]() ,且
,且![]() 对任意正整数都成立,数列{
对任意正整数都成立,数列{![]() }的前n项和为Sn。
}的前n项和为Sn。
(1)若![]() ,且
,且![]() ,求a;
,求a;
(2)是否存在实数k,使数列{![]() }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项![]() 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100〕后画出如图所示的频率分布直方图.观察图形给出的信息,回答下列问题: 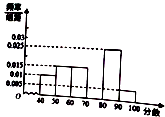
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足:a1= ![]() ,a1 , a2 , a3﹣
,a1 , a2 , a3﹣ ![]() 成等差数列,公比q∈(0,1)
成等差数列,公比q∈(0,1)
(1)求数列{an}的通项公式;
(2)设bn=2nan , 求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 能构成映射,下列说法正确的有 ( )
能构成映射,下列说法正确的有 ( )
(1)A中的任一元素在B中必须有像且唯一;
(2)A中的多个元素可以在B中有相同的像;
(3)B中的多个元素可以在A中有相同的原像;
(4)像的集合就是集合B.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com