
| ||
| 2 |
| PF |
| EF |
| ||
| 2 |
| PQ |
| AQ |
| AQ |
| PQ |
| AQ |
| PQ |
| ||||
|
|
| 2a2 | ||||
|
| ||
| 3 |
| AQ |
| PQ |
| ||
| 2 |


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
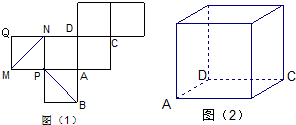
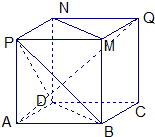
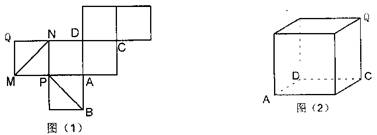
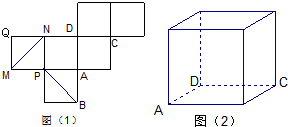 如图(1)是一正方体的表面展开图,MN和PB是两条对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题.
如图(1)是一正方体的表面展开图,MN和PB是两条对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2007•揭阳二模)如图(1)是一正方体的表面展开图,MN和PB是两条面对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题.
(2007•揭阳二模)如图(1)是一正方体的表面展开图,MN和PB是两条面对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题.查看答案和解析>>
科目:高中数学 来源:2011届湖北省襄阳五中高三第四次模拟考试文科数学 题型:解答题
(本小题满分12分)
如图(1)是一正方体的表面展开图,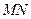 和
和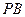 是两条面对角线,请在图(2)的正方体中将
是两条面对角线,请在图(2)的正方体中将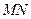 和
和 画出来,并就这个正方体解决下面问题.
画出来,并就这个正方体解决下面问题.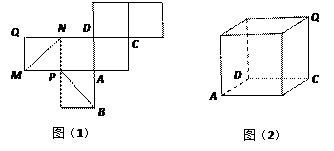
(Ⅰ)求证: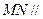 平面
平面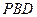 ;
;
(Ⅱ)求证: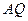 ⊥平面
⊥平面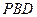 ;
;
(Ⅲ)求二面角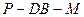 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2011年湖南省高三第一次学情摸底考试数学卷 题型:解答题
(本小题满分13 分)
如图(1)是一正方体的表面展开图,MN 和PB 是两条面对角线,请在图(2)的正方体中将MN 和PB 画出来,并就这个正方体解决下面问题。
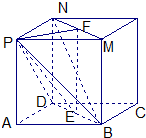
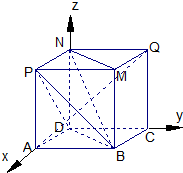
(1)求证:MN//平面PBD;
(2)求证:AQ⊥平面PBD;
(3)求二面角P—DB—M 的大小.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高三寒假作业数学卷一 题型:解答题
(14 分)如图(1)是一正方体的表面展开图,MN 和PB 是两条面对角线,请在图(2)的正方体中将MN 和PB 画出来,并就这个正方体解决下面问题。
(1)求证:MN//平面PBD;
(2)求证:AQ⊥平面PBD;
(3)求二面角P—DB—M 的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com