
【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
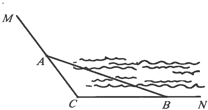
(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】三角形的面积为![]() ,其中
,其中![]() ,
,![]() ,
,![]() 为三角形的边长,
为三角形的边长,![]() 为三角形内切圆的半径,则利用类比推理,可得出四面体的体积为( )
为三角形内切圆的半径,则利用类比推理,可得出四面体的体积为( )
A. ![]()
B. ![]()
C. ![]() ,(
,(![]() 为四面体的高)
为四面体的高)
D. ![]() ,(
,(![]() ,
,![]() ,
,![]() ,
,![]() 分别为四面体的四个面的面积,
分别为四面体的四个面的面积,![]() 为四面体内切球的半径)
为四面体内切球的半径)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感市旅游局为了了解双峰山景点在大众中的熟知度,从年龄在15~65岁的人群中随机抽取n人进行问卷调查,把这n人按年龄分成5组:第一组[15,25),第二组[25,35),第三组[35,45),第四组[45,55),第五组[55,65],得到的样本的频率分布直方图如右:

调查问题是“双峰山国家森林公园是几A级旅游景点?”每组中回答正确的人数及回答正确的人数占本组的频率的统计结果如下表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | y | 0.9 |
第4组 | [45,55) | 9 | a |
第5组 | [55,65] | 7 | b |
(1)分别求出n,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人;
(3)在(2)抽取的6人中随机抽取2人,求所抽取的两人来自不同年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
①![]() 的单调递减区间;
的单调递减区间;
②当![]() 时,直线y=k与y=f (x)的图象有两个不同交点;
时,直线y=k与y=f (x)的图象有两个不同交点;
③函数y=f(x)的图象与![]() 的图象没有公共点;
的图象没有公共点;
④当![]() 时,函数
时,函数![]() 的最小值为2.
的最小值为2.
其中正确结论的序号是_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(Ⅰ)若曲线![]() 与曲线
与曲线![]() 在它们的某个交点处具有公共切线,求
在它们的某个交点处具有公共切线,求![]() 的值;
的值;
(Ⅱ)若存在实数![]() 使不等式
使不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的取值范围
的取值范围![]()
(Ⅲ)若方程![]() 有三个不同的解
有三个不同的解![]() ,且它们可以构成等差数列,写出实数
,且它们可以构成等差数列,写出实数![]() 的值(只需写出结果).
的值(只需写出结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生物兴趣小组对冬季昼夜温差与反季节新品种大豆发芽数之间的关系进行研究,他们分别记录了![]() 月
月![]() 日至
日至![]() 月
月![]() 日每天的昼夜温差与实验室每天
日每天的昼夜温差与实验室每天![]() 颗种子的发芽数,得到以下表格
颗种子的发芽数,得到以下表格

该兴趣小组确定的研究方案是:先从这![]() 组数据中选取
组数据中选取![]() 组数据,然后用剩下的
组数据,然后用剩下的![]() 组数据求线性回归方程,再用被选取的
组数据求线性回归方程,再用被选取的![]() 组数据进行检验.
组数据进行检验.
(1) 求统计数据中发芽数的平均数与方差;
(2) 若选取的是![]() 月
月![]() 日与
日与![]() 月
月![]() 日的两组数据,请根据
日的两组数据,请根据![]() 月
月![]() 日至
日至![]() 月
月![]() 日的数据,求出发芽数
日的数据,求出发芽数![]() 关于温差
关于温差![]() 的线性回归方程
的线性回归方程![]() ,若由线性回归方程得到的估计数据与所选取的检验数据的误差不超过
,若由线性回归方程得到的估计数据与所选取的检验数据的误差不超过![]() ,则认为得到的线性回归方程是可靠的,问得到的线性回归方程是否可靠? 附:线性回归方程
,则认为得到的线性回归方程是可靠的,问得到的线性回归方程是否可靠? 附:线性回归方程![]() 中斜率和截距最小二乘估法计算公式:
中斜率和截距最小二乘估法计算公式:
 ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com