
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.

(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有97.5%的把握认为潜伏期长短与患者年龄有关;
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |
(3)研究发现,某药物对新冠病毒有一定的抑制作用,需要在抽取的300人中分层选取7位60岁以下的患者做Ⅰ期临床试验,再从选取的7人中随机抽取两人做Ⅱ期临床试验,求两人中恰有1人为“长潜伏者”的概率.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

【答案】(1)平均数为![]() ,“长潜伏者”的人数为
,“长潜伏者”的人数为![]() 人
人
(2)列联表见解析,有97.5%的把握认为潜伏期长短与年龄有关
(3)![]()
【解析】
(1)根据频率分布直方图中的数据计算即可
(2)首先将列联表补充完整,然后计算出![]() 的观测值即可
的观测值即可
(3)由分层抽样知7人中,“短潜伏者”有3人,记为![]() ,“长潜伏者”有4人,记为D,E,F,G, 然后列举出所有的情况,然后数出满足所求事件的基本事件的个数即可.
,“长潜伏者”有4人,记为D,E,F,G, 然后列举出所有的情况,然后数出满足所求事件的基本事件的个数即可.
(1)平均数![]() .
.
“长潜伏者”即潜伏期时间不低于6天的频率为0.5
所以500人中“长潜伏者”的人数为![]() 人
人
(2)由题意补充后的列联表如图:
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | 70 | 160 |
60岁以下 | 60 | 80 | 140 |
合计 | 150 | 150 | 300 |
所以![]() 的观测值为
的观测值为![]() ,
,
经查表,得![]() ,所以有97.5%的把握认为潜伏期长短与年龄有关.
,所以有97.5%的把握认为潜伏期长短与年龄有关.
(3)由分层抽样知7人中,“短潜伏者”有3人,记为![]() ,“长潜伏者”有4人,记为D,E,F,G,
,“长潜伏者”有4人,记为D,E,F,G,
从中抽取2人,共有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
共有21种不同的结果,两人中恰好有1人为“长潜伏者”包含了12种结果.
所以所求概率![]() .
.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】动圆![]() 过定点
过定点![]() ,且在
,且在![]() 轴上截得的弦
轴上截得的弦![]() 的长为4.
的长为4.
(1)若动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(2)在曲线![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使过点
,使过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 的交点
的交点![]() 满足
满足![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标及定值;若不存在,请说明理由.
的坐标及定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网购人数的日益增多,网上的支付方式也呈现一种多样化的状态,越来越多的便捷移动支付方式受到了人们的青睐,更被网友们评为“新四大发明”之一.随着人们消费观念的进步,许多人喜欢用信用卡购物,考虑到这一点,一种“网上的信用卡”横空出世——蚂蚁花呗.这是一款支付宝和蚂蚁金融合作开发的新支付方式,简单便捷,同时也满足了部分网上消费群体在支付宝余额不足时的“赊购”消费需求.为了调查使用蚂蚁花呗“赊购”消费与消费者年龄段的关系,某网站对其注册用户开展抽样调查,在每个年龄段的注册用户中各随机抽取100人,得到各年龄段使用蚂蚁花呗“赊购”的人数百分比如图所示.

(1)由大数据可知,在18到44岁之间使用花呗“赊购”的人数百分比y与年龄x成线性相关关系,利用统计图表中的数据,以各年龄段的区间中点代表该年龄段的年龄,求所调查群体各年龄段“赊购”人数百分比y与年龄x的线性回归方程(回归直线方程的斜率和截距保留两位有效数字);
(2)该网站年龄为20岁的注册用户共有2000人,试估算该网站20岁的注册用户中使用花呗“赊购”的人数;
(3)已知该网店中年龄段在18-26岁和27-35岁的注册用户人数相同,现从18到35岁之间使用花呗“赊购”的人群中按分层抽样的方法随机抽取8人,再从这8人中简单随机抽取2人调查他们每个月使用花呗消费的额度,求抽取的两人年龄都在18到26岁的概率.
参考答案: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是自然对数的底数,函数
是自然对数的底数,函数![]() 与
与![]() 的定义域都是
的定义域都是![]() .
.
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)判断函数![]() 零点个数;
零点个数;
(3)用![]() 表示
表示![]() 的最小值,设
的最小值,设![]() ,
,![]() ,若函数
,若函数![]() 在
在![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别是离心率
分别是离心率![]() 的椭圆
的椭圆![]() 的左右项点,P是椭圆E的上顶点,且
的左右项点,P是椭圆E的上顶点,且![]() .
.
(1)求椭圆E的方程;
(2)若动直线![]() 过点
过点![]() ,且与椭圆E交于A、B两点,点M与点B关于y轴对称,求证:直线
,且与椭圆E交于A、B两点,点M与点B关于y轴对称,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
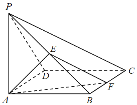
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的动点.
上的动点.
(1)求证:平面![]() 平面
平面![]() .
.
(2)试确定点![]() 的位置,使平面
的位置,使平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】丑橘是人们日常生活中常见的营养型水果.某地水果批发市场销售来自5个不同产地的丑橘,各产地的包装规格相同,它们的批发价格(元/箱)和市场份额如下:
产地 |
|
|
|
|
|
批发价格 | 150 | 160 | 140 | 155 | 170 |
市场份额 |
|
|
|
|
|
市场份额亦称“市场占有率”.指某一产品的销售量在市场同类产品中所占比重.
(1)从该地批发市场销售的丑橘中随机抽取一箱,估计该箱丑橘价格低于160元的概率;
(2)按市场份额进行分层抽样,随机抽取20箱丑橘进行检验,①从产地![]() ,
,![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;②从这
的值;②从这![]() 箱中随机抽取三箱进行等级检验,随机变量
箱中随机抽取三箱进行等级检验,随机变量![]() 表示来自产地
表示来自产地![]() 的箱数,求
的箱数,求![]() 的分布列和数学期望.
的分布列和数学期望.
(3)产地![]() 的丑橘明年将进入该地市场,定价160元/箱,并占有一定市场份额,原有五个产地的丑橘价格不变,所占市场份额之比不变(不考虑其他因素).设今年丑橘的平均批发价为每箱
的丑橘明年将进入该地市场,定价160元/箱,并占有一定市场份额,原有五个产地的丑橘价格不变,所占市场份额之比不变(不考虑其他因素).设今年丑橘的平均批发价为每箱![]() 元,明年丑橘的平均批发价为每箱
元,明年丑橘的平均批发价为每箱![]() 元,比较
元,比较![]() ,
,![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四棱锥![]() 中,已知异面直线
中,已知异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,给出下面三个命题:
,给出下面三个命题:
![]() :若
:若![]() ,则此四棱锥的侧面积为
,则此四棱锥的侧面积为![]() ;
;
![]() :若
:若![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 平面
平面![]() ;
;
![]() :若
:若![]() 都在球
都在球![]() 的表面上,则球
的表面上,则球![]() 的表面积是四边形
的表面积是四边形![]() 面积的
面积的![]() 倍.
倍.
在下列命题中,为真命题的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作.其中的一道题“今有木,方三尺,高三尺,欲方五寸作枕一枚.问:得几何?”意思是:“有一块棱长为3尺的正方体方木,要把它作成边长为5寸的正方体枕头,可作多少个?”现有这样的一个正方体木料,其外周已涂上油漆,则从切割后的正方体枕头中任取一块,恰有一面涂上油漆的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com