
【题目】已知数列{an}的前n项和为Sn , 且满足a1=1,nSn+1﹣(n+1)Sn= ![]() ,n∈N*
,n∈N*
(1)求a2的值;
(2)求数列{an}的通项公式.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3x2﹣9x+1(x∈R).
(1)求函数f(x)的单调区间.
(2)若f(x)﹣2a+1≥0对x∈[﹣2,4]恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市出租车的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9 元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85(元/km)).
(1)将某乘客搭乘一次出租车的费用f(x)(单位:元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客的行程为16 km,他准备先乘一辆出租车行驶8 km后,再换乘另一辆出租车完成余下行程,请问:他这样做是否比只乘一辆出租车完成全部行程更省钱?
(现实中要计等待时间且最终付费取整数,本题在计算时都不予考虑)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: ![]() =
= 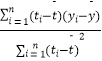 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥P—ABCD中,∠ABC=60°,PA=AC=a,PB=PD= ![]() ,点E是PD的中点.
,点E是PD的中点.
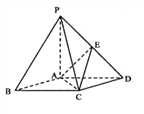
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)求二面角E—AC—D的大小;
(Ⅲ)求点P到平面EAC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com