
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]()
![]() ,
, ![]() 平面
平面![]() ,
, ![]() .设
.设![]() 分别为
分别为![]() 的中点.
的中点.

(1)求证:平面![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)证明![]() ,推出
,推出![]() 平面
平面![]() ,证明
,证明![]() ,即可证明
,即可证明![]() 平面
平面![]() ,然后证明平面
,然后证明平面![]() 平面
平面![]() ;(2)以点
;(2)以点![]() 为原点,
为原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的法向量,平面
的法向量,平面![]() 的法向量,利用空间向量的数量积求解面角
的法向量,利用空间向量的数量积求解面角![]() 的平面角的余弦值.
的平面角的余弦值.
试题解析:(1)证明:∵![]() 、
、![]() 分别为
分别为![]() ,
, ![]() 的中点, 则
的中点, 则![]() .又∵
.又∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .在
.在![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∴
,∴![]() .∵
.∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,又∵
,又∵![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,又∵
,又∵![]() ,平面
,平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,

如图,以点![]() 为原点,
为原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴建立空间直角坐标系,∴
轴建立空间直角坐标系,∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ∴
∴![]() ,设
,设![]() 是平面
是平面![]() 的法向量,则
的法向量,则![]() ,即
,即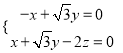 ,可取
,可取![]() ,又平面
,又平面![]() 的法向量为
的法向量为![]() ,∴
,∴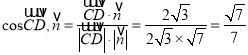 ,由图可知,二面角
,由图可知,二面角![]() 的平面角为锐角,∴二面角
的平面角为锐角,∴二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义在R上的偶函数,对于x∈R,都有f(x+4)=f(x)+f(2)成立,当x1,x2∈[0,2]且x1≠x2时,都有![]() 给出下列四个命题:
给出下列四个命题:
①f(﹣2)=0;
②直线x=﹣4是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[4,6]上为减函数;
④函数y=f(x)在(﹣8,6]上有四个零点.
其中所有正确命题的序号为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|1<x<3},集合B={x|2m<x<1-m}.
(1)当m=-1时,求A∪B;
(2)若AB,求实数m的取值范围;
(3)若A∩B=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间; 
(2)写出函数f(x)的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市五一假期举行促销活动,规定一次购物不超过100元的不给优惠;超过100元而不超过300元时,按该次购物全额9折优惠;超过300元的其中300 元仍按9折优惠,超过部分按8折优惠.
(1)写出顾客购物全额与应付金额之间的函数关系,并画出流程图,要求输入购物全额,能输出应付金额.
(2)若某顾客的应付金额为282.8元,请求出他的购物全额.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com