
分析 先求出C的轨迹方程,再求出A与圆心的距离,即可求出线段AC长度的最小值.
解答 解:设C(x,y),则
∵$\overrightarrow{OC}$•$\overrightarrow{PC}$=-7,
∴(x,y)•(x-6,y)=-7,
∴x2-6x+y2=-7,
∴(x-3)2+y2=2
设A(a,b),则A与圆心的距离为$\sqrt{(a-3)^{2}+{b}^{2}}$=$\sqrt{(a-3)^{2}+4a}$=$\sqrt{(a-1)^{2}+8}$≥2$\sqrt{2}$,
∴线段AC长度的最小值为2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查线段AC长度的最小值,考查圆的方程,确定C的轨迹方程是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (-∞,-3) | C. | ($\sqrt{2}$,2) | D. | (-8,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
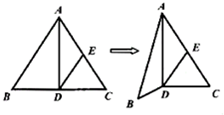 如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )
如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com