
【题目】已知函数f(x)=x+ ![]() 是奇函数.
是奇函数.
(1)若点Q(1,3)在函数f(x)的图象上,求函数f(x)的解析式;
(2)写出函数f(x)的单调区间(不要解答过程,只写结果);
(3)设点A(t,0),B(t+1,0)(t∈R),点P在f(x)的图象上,且△ABP的面积为2,若这样的点P恰好有4个,求实数a的取值范围.
【答案】
(1)解:函数f(x)=x+ ![]() 是奇函数,则f(x)+f(﹣x)=0恒成立,即x+
是奇函数,则f(x)+f(﹣x)=0恒成立,即x+ ![]() b=0.∴f(x)=x+
b=0.∴f(x)=x+ ![]() (a>0).
(a>0).
∵Q(1,3)在函数f(x)的图象上,∴1+a=3,∴a=2,∴f(x)=x+ ![]() .(x≠0).
.(x≠0).
(2)解:f(x)=x+ ![]() (a>0).的增区间为:(﹣∞,﹣
(a>0).的增区间为:(﹣∞,﹣ ![]() ),(
),( ![]() ,+∞);减区间为:(﹣
,+∞);减区间为:(﹣ ![]() ,0),(0,
,0),(0, ![]() ).
).
(3)解:∵点A(t,0),B(t+1,0)(t∈R)在横轴上,且AB=1,
∴在f(x)的图象上恰好有4个点,使△ABP的面积为2在f(x)的图象上恰好有4个点到横轴的距离等于4,
如图所示,函数f(x)的图象与y=4,y=﹣4各有两个交点,即f(x)min<4,2 ![]() <4,解得0<a<4.
<4,解得0<a<4.
∴实数a的取值范围为:(0,4).

【解析】(1)f(x)+f(﹣x)=0恒成立,可得b=0.Q(1,3)在函数f(x)的图象上,可得a=2即可. (2)由对勾函数图象可得;(3)在f(x)的图象上恰好有4个点,使△ABP的面积为2在f(x)的图象上恰好有4个点到横轴的距离等于4,即f(x)min<4,2 ![]() <4,解得a.
<4,解得a.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,已知A(﹣2,0),直角顶点B(0,﹣2 ![]() ),点C在x轴上.
),点C在x轴上. 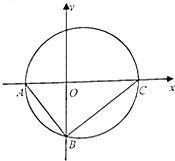
(Ⅰ)求Rt△ABC外接圆的方程;
(Ⅱ)求过点(﹣4,0)且与Rt△ABC外接圆相切的直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2xsinθ﹣1,x∈[﹣ ![]() ,
, ![]() ].
].
(1)当 ![]() 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若函数f(x)在x∈[﹣ ![]() ,
, ![]() ]上是单调增函数,且θ∈[0,2π],求θ的取值范围.
]上是单调增函数,且θ∈[0,2π],求θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),当x≥0时, f(x)= ![]() ,
,
则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
A.1﹣2a
B.2a﹣1
C.1﹣2﹣a
D.2﹣a﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电力部门需在A、B两地之间架设高压电线,因地理条件限制,不能直接测量A、B两地距离.现测量人员在相距 ![]() km的C、D两地(假设A、B、C、D在同一平面上)测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度为A、B距离的
km的C、D两地(假设A、B、C、D在同一平面上)测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度为A、B距离的 ![]() 倍,问施工单位应该准备多长的电线?
倍,问施工单位应该准备多长的电线? 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点. 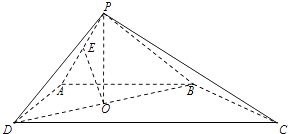
(1)求证:PO⊥平面ABCD;
(2)若E为线段PA上一点,且 ![]() ,求二面角P﹣OE﹣C的余弦值.
,求二面角P﹣OE﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com