
【题目】已知函数![]() .
.
(1)求函数的定义域;
(2)判断函数的奇偶性,并证明你的结论;
(3)在函数![]() 图像上是否存在两个不同的点
图像上是否存在两个不同的点![]() ,使直线
,使直线![]() 垂直
垂直![]() 轴,若存在,求出
轴,若存在,求出![]() 两点坐标;若不存在,说明理由.
两点坐标;若不存在,说明理由.
【答案】(1) 函数![]() 的定义域为
的定义域为![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题分析:(1)根据函数的解析式有意义的原则,结合对数的真数部分必须大于0,构造关于x的不等式组,解不等式组,即可得到答案;
(2)根据函数奇偶性的定义,利用对数的运算性质,判断f(﹣x)与f(x)的关系,即可得到函数f(x)的奇偶性;
(3) 假设函数![]() 图象上存在两点A(
图象上存在两点A(![]() ,
,![]() ),
),![]() , 使直线
, 使直线![]() 垂直
垂直![]() 轴,则
轴,则![]() ,
,
经推理不成立,故不存在.
试题解析:
(1) 由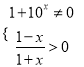
![]() ,
,
∴ 函数![]() 的定义域为
的定义域为![]()
(2) ∵f (-x)= ![]() + lg
+ lg![]() =
=![]() – lg
– lg![]() =-f (x),
=-f (x),
∴ f (x)是奇函数
(3)假设函数![]() 图象上存在两点A(
图象上存在两点A(![]() ,
,![]() ),
),![]() ,
,
使直线AB恰好与y轴垂直,其中![]() .
.
即当![]() 时,
时, ![]() , 不妨设
, 不妨设![]() ,
,![]()
于是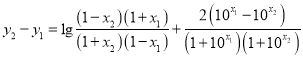
由![]()
![]()
![]()
又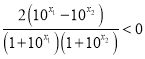
![]() , ∴
, ∴![]() , 与
, 与![]() =
=![]() 矛盾.
矛盾.
故函数![]() 图象上不存在两个不同的点A、B,使直线AB垂直y轴.
图象上不存在两个不同的点A、B,使直线AB垂直y轴.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣x2+1. (Ⅰ)若曲线y=f(x)在x=1处的切线方程为4x﹣y+b=0,求实数a和b的值;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)若a<0,且对任意x1 , x2∈(0,+∞),x1≠x2 , 都有|f(x1)﹣f(x2)|>|x1﹣x2|,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(![]() +x)cos(
+x)cos(![]() -x),g(x)=
-x),g(x)=![]() sin 2x-
sin 2x-![]() .
.
(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象如图所示,为了得到函数
的图象如图所示,为了得到函数![]() 的图象,可以把函数
的图象,可以把函数![]() 的图象( )
的图象( )
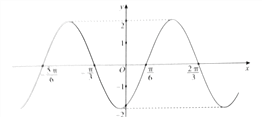
A. 每个点的横坐标缩短到原来的![]() (纵坐标不变),再向左平移
(纵坐标不变),再向左平移![]() 个单位
个单位
B. 每个点的横坐标缩短到原来的2倍(纵坐标不变),再向左平移![]() 个单位
个单位
C. 先向左平移![]() 个单位,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)
个单位,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)
D. 先向左平移![]() 个单位,再把所得各点的横坐标伸长到原来的
个单位,再把所得各点的横坐标伸长到原来的![]() (纵坐标不变)
(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE= ![]() CD=2,M是线段AE上的动点.
CD=2,M是线段AE上的动点. 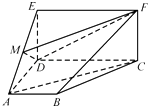
(Ⅰ)试确定点M的位置,使AC∥平面MDF,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面MDF将几何体ADE﹣BCF分成的两部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段![]() 的端点
的端点![]() ,端点
,端点![]() 在圆
在圆![]() 上运动
上运动
(Ⅰ)求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
(Ⅱ) 设动直线![]() 与圆
与圆![]() 交于
交于![]() 两点,问在
两点,问在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称?若存在,请求出点
轴对称?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com