
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别相交于点B、C,经过B、C两点的抛物线
轴分别相交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一交点为A,顶点为P,且对称轴为直线
轴的另一交点为A,顶点为P,且对称轴为直线![]() .
.
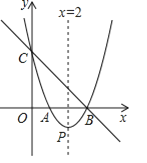
(1)求该抛物线的函数表达式;
(2)连结AC.请问在![]() 轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=x2-4x+3;(2)存在,(0,0),(![]() ,0)
,0)
【解析】
(1)先由直线解析式求出B,C两点坐标,再根据对称轴为直线![]() 可求出点A的坐标,A,B,C三点坐标代入
可求出点A的坐标,A,B,C三点坐标代入![]() ,可得抛物线的函数式;(2)设抛物线的对称轴交x轴于点M,由
,可得抛物线的函数式;(2)设抛物线的对称轴交x轴于点M,由![]() 可知
可知![]() ,由
,由![]() 可知
可知![]() ,由相似三角形对应边的比相等可求出点Q。
,由相似三角形对应边的比相等可求出点Q。

解:(1)∵直线y=-x+3与x轴相交于点B,∴当y=0时,x=3.
∴点B的坐标为![]() .
.
又∵抛物线过x轴上的A,B两点,且对称轴为x=2,
根据抛物线的对称性,∴点A的坐标为(1,0).
∵y=-x+3过点C,易知![]() ,∴c=3.
,∴c=3.
又∵抛物线![]() 过点
过点![]() ,
,![]() ,
,
∴![]() 解得
解得![]() ∴
∴![]()
(2)设在x轴上存在点Q.连结PB,由![]() ,得
,得![]() .
.
设抛物线的对称轴交x轴于点M.
在Rt△PBM中,PM=MB=1,∴△PBM为等腰直角三角形.∴![]() .
.
由点![]() ,
,![]() ,可得OB=OC=3,∴△OBC为等腰直角三角形.∴
,可得OB=OC=3,∴△OBC为等腰直角三角形.∴![]() .
.
由勾股定理,得![]() .
.
假设在x轴上存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似.
①当![]() ,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
即![]() ,∴BQ=3.∴Q1的坐标是(0,0).
,∴BQ=3.∴Q1的坐标是(0,0).
②当![]() ,∠QBP=∠ABC=45°时,△QBP∽△ABC,
,∠QBP=∠ABC=45°时,△QBP∽△ABC,
即![]() ,∴QB=
,∴QB=![]() .∴Q2的坐标是(
.∴Q2的坐标是(![]() ,0).
,0).
由题意知点Q不可能在B点右侧的x轴上.综上所述,在x轴上存在两点Q1(0,0),Q2(![]() ,0)
,0)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】数学是研究数量、结构、变化、空间以及信息等概念的一门科学.在人类历史发展和社会生活中,数学发挥着不可替代的作用,也是学习和研究现代科学技术必不可少的基本工具.
(1)为调查大学生喜欢数学命题是否与性别有关,随机选取![]() 名大学生进行问卷调查,当被调查者问卷评分不低于
名大学生进行问卷调查,当被调查者问卷评分不低于![]() 分则认为其喜欢数学命题,当评分低于
分则认为其喜欢数学命题,当评分低于![]() 分则认为其不喜欢数学命题,问卷评分的茎叶图如下:
分则认为其不喜欢数学命题,问卷评分的茎叶图如下:
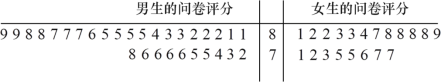
依据上述数据制成如下列联表:
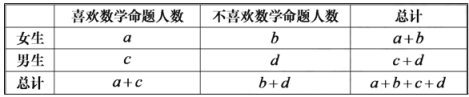
请问是否有![]() 的把握认为大学生是否喜欢数学命题与性别有关?
的把握认为大学生是否喜欢数学命题与性别有关?
参考公式及数据:![]() .
.
|
|
|
|
|
|
|
|
|
|
(2)在某次命题大赛中,![]() 同学要进行
同学要进行![]() 轮命题,其在每轮命题成功的概率均为
轮命题,其在每轮命题成功的概率均为![]() ,各轮命题相互独立,若该同学在
,各轮命题相互独立,若该同学在![]() 轮命题中恰有
轮命题中恰有![]() 次成功的概率为
次成功的概率为![]() ,记该同学在
,记该同学在![]() 轮命题中的成功次数为
轮命题中的成功次数为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,点
,点![]() ,
,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上的动点,且满足
上的动点,且满足![]() .
.
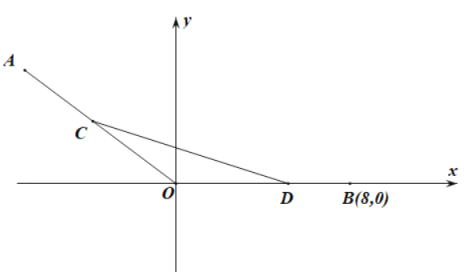
(1)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的外接圆的一般方程,并求
的外接圆的一般方程,并求![]() 的外接圆所过定点的坐标.
的外接圆所过定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为6,且椭圆
的长轴长为6,且椭圆![]() 与圆
与圆![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点P(0,1)作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
,![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形,若存在,求出点
为底边的等腰三角形,若存在,求出点![]() 的横坐标的取值范围;若不存在,请说明理由.
的横坐标的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某环线地铁按内、外环线同时运行,内、外环线的长均为30千米(忽略内、外环线长度差异).
(1)当9列列车同时在内环线上运行时,要使内环线乘客最长候车时间为10分钟,求内环线列车的最小平均速度;
(2)新调整的方案要求内环线列车平均速度为25千米/小时,外环线列车平均速度为30千米/小时.现内、外环线共有18列列车全部投入运行,要使内外环线乘客的最长候车时间之差不超过1分钟,向内、外环线应各投入几列列车运行?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是单调递增函数,其反函数是
是单调递增函数,其反函数是![]() .
.
(1)若![]() ,求
,求![]() 并写出定义域
并写出定义域![]() ;
;
(2)对于⑴的![]() 和
和![]() ,设任意
,设任意![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)已知函数![]() 和
和![]() 的图象有交点,求证:它们的交点一定在直线
的图象有交点,求证:它们的交点一定在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列出了如表并给出了部分数据:
在某一个周期内的图象时,列出了如表并给出了部分数据:
| 0 |
| π |
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
(1)请根据上表数据,写出函数![]() 的解析式;(直接写出结果即可)
的解析式;(直接写出结果即可)
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)设![]() ,已知函数
,已知函数![]() 在区间
在区间![]() 上的最大值是img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/20/139c9676/SYS202011262014544768390673_ST/SYS202011262014544768390673_ST.013.png" width="24" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,求t的值以及函数
上的最大值是img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/20/139c9676/SYS202011262014544768390673_ST/SYS202011262014544768390673_ST.013.png" width="24" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,求t的值以及函数![]() 在区间[
在区间[![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.

(1)求出第4组的频率,并补全频率分布直方图;
(2)根据样本频率分布直方图估计样本的中位数与平均数;
(3)如果用分层抽样的方法从“优秀”和“良好”的学生中共选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com