(本题满分12分)已知△

的三个内角
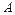
、
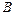
、
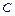
所对的边分别为
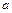
、
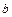
、
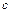
.
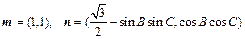
,且
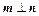
.(1)求
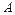
的大小;(2)若
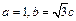
.求
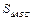
.
解:(1)因为

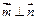
,所以

,……2分
所以
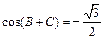
,即
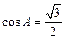
, …………………4分
因为
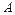
为
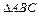
的内角,所以
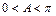
, …………………5分
所以
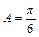
. ………………6分
(2)若
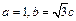
.由余弦定理得
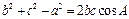
,所以得
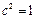
, ……………………10分
所以
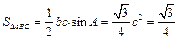
………………12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本题满分12分)已知函数
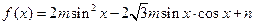
的定义域为
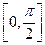
,值域为
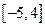
.试求函数
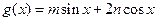
(
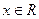
)的最小正周期和最值
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
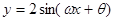
为偶函数
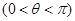
,其图像与直线
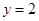
的某两个交点的横坐标为
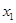
,
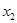
,若
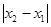
的最小值为
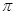
,则( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设
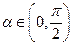
,函数
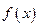
的定义域为
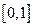
且
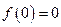
,
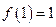
当
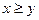
时有
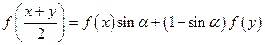
(1)求
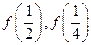
;
(2)求
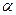
的值;
(3)求函数
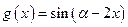
的单调区间.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数

(A>0,0<

<π)在

时取最大值4 (10分)
(1)求

的最小正周期
(2)求

的解析式
(3)把


的图像按向量

平移后得函数

的图像,求函数

的解析式
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(10分) 已知函数
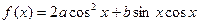
,
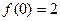
,
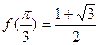
(1)求
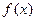
的最大值和最小值;
(2)求
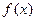
的单调递增区间
(3)对于角
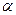
,
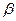
,若有
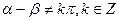
,且
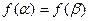
,求
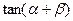
的值
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
在
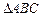
中,角A,B,C

所对的边分别为
a,b,c,若
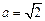
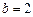
,
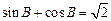
,
则角A的大小为
。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分12分)已知向量


函数

.
(Ⅰ)求函数

的解析式,并写出函数

的周期与对称中心坐标;
(Ⅱ)求函数

的单调递增区间.
查看答案和解析>>

 的三个内角
的三个内角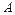 、
、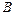 、
、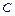 所对的边分别为
所对的边分别为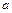 、
、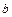 、
、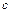 .
.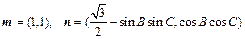 ,且
,且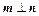 .(1)求
.(1)求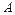 的大小;(2)若
的大小;(2)若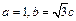 .求
.求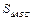 .
. 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案 (A>0,0<
(A>0,0< <π)在
<π)在 时取最大值4 (10分)
时取最大值4 (10分) 的最小正周期
的最小正周期 的解析式
的解析式
 的图像按向量
的图像按向量 平移后得函数
平移后得函数 的图像,求函数
的图像,求函数 的解析式
的解析式