函数y=lgsinx的单调递减区间为________.
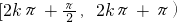
分析:由sinx>0可得函数的定义域,由复合函数的单调性及由函数的定义域求解出函数的单调递减区间
解答:由题意可得函数的定义域为{x|2kπ<x<2kπ+π},k∈Z
∵函数y=lgt在其定义域内单调递增
∴原函数y=lgsinx的单调递减区间即为函数y=sinx在(2kπ,2k+π),k∈Z上的单调递减区间
∴
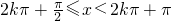
,k∈Z
故答案为:
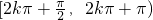
,k∈Z
点评:本题考查了对数函数和正弦函数复合而成的函数,分别利用它们的性质以及复合函数的单调性求解,注意要求原函数的定义域,这是解答中容易忽视的地方.

 中考解读考点精练系列答案
中考解读考点精练系列答案