已知函数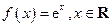
．
(1)若直线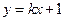
与
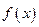的反函数的图象相切，求实数k的值;
(2)设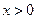
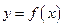，讨论曲线
与曲线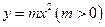
公共点的个数;
(3)设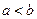
，比较
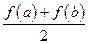与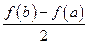
的大小，并说明理由．
名师点睛字词句段篇系列答案科目：高中数学 来源： 题型：解答题
（2013•浙江）已知a∈R，函数f（x）=2x3﹣3（a+1）x2+6ax
（Ⅰ）若a=1，求曲线y=f（x）在点（2，f（2））处的切线方程；
（Ⅱ）若|a|＞1，求f（x）在闭区间[0，|2a|]上的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
根据统计资料，某工艺品厂的日产量最多不超过20件，每日产品废品率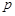
与日产量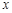
(件)之间近似地满足关系式
(日产品废品率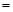
)．已知每生产一件正品可赢利2千元，而生产一件废品则亏损1千元．（该车间的日利润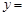
日正品赢利额
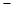日废品亏损额）
（1）将该车间日利润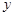
(千元)表示为日产量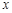(件)的函数；
（2）当该车间的日产量为多少件时，日利润最大？最大日利润是几千元？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
一个圆柱形圆木的底面半径为1m，长为10m，将此圆木沿轴所在的平面剖成两个部分．现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形
（如图所示，其中O为圆心，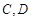
在半圆上），设
，木梁的体积为V（单位：m3），表面积为S（单位：m2）．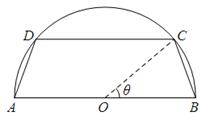
（1）求V关于θ的函数表达式；
（2）求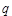
的值，使体积V最大；
（3）问当木梁的体积V最大时，其表面积S是否也最大？请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的单调区间；
恰有两个交点，求
的取值范围．
(
)
在点
处的切线方程为
，求
上存在极值点，求实数
的取值范围．
在区间
，
上有极大值
．
在区间
.
的单调性；
，求
上的最大值；
，不等式
都成立（其中
是自然对数的底数）．
在(0，1)上单调递减．
，求
在[1，2]上的最小值．