
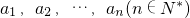 ,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.
,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”. ,k=1,2,….
,k=1,2,…. ,则
,则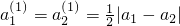 ,即经T1(c1)后,前两项相等;
,即经T1(c1)后,前两项相等; ,则
,则 ,即经T2(c2)后,前3项相等;
,即经T2(c2)后,前3项相等;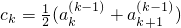 ,变换后数列变为
,变换后数列变为 ,则
,则 ;
; ,
,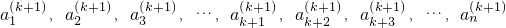 ,
, ;
; ;
;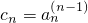 ,经过变换Tn(cn)后,数列各项均为0.
,经过变换Tn(cn)后,数列各项均为0. )
) ,i=1,2,…,k.
,i=1,2,…,k. ≥(k+1)k+1-k•kk>0
≥(k+1)k+1-k•kk>0 .取
.取 ,
, ,继续做类似的变换,取
,继续做类似的变换,取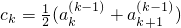 ,(k≤n-1),经Tk(ck)后,得到数列的前k+1项相等,再取
,(k≤n-1),经Tk(ck)后,得到数列的前k+1项相等,再取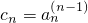 ,经Tn(cn)后,即可得到结论;
,经Tn(cn)后,即可得到结论;

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市朝阳区高三(上)期中数学试卷(理科)(解析版) 题型:解答题
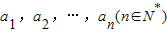 ,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.
,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市朝阳区高三(上)期中数学试卷(理科)(解析版) 题型:解答题
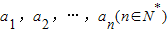 ,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.
,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市朝阳区高三(上)期中数学试卷(文科)(解析版) 题型:解答题
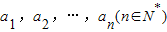 ,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”
,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com