
 m,盖子边长为
m,盖子边长为 m,
m,
 关于
关于 的解析式;
的解析式; 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 万元,年维修费用第一年是
万元,年维修费用第一年是 万元,第二年是
万元,第二年是 万元,第三年是
万元,第三年是 万元,…,以后逐年递增
万元,…,以后逐年递增 万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用
万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用 年的维修费用的和为
年的维修费用的和为 ,年平均费用为
,年平均费用为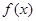 .
. ,
,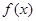 的解析式;
的解析式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 月份 | 用气量(立方米) | 煤气费(元) |
| 1 | 4 | 4.00 |
| 2 | 25 | 14.00 |
| 3 | 35 | 19.00 |
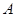
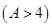 立方米时,只付基本费3元+每户每月定额保险费
立方米时,只付基本费3元+每户每月定额保险费
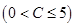 元;若用气量超过
元;若用气量超过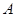 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付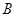 元.
元.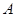 、
、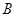 、
、 的值;
的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com