
 ,
, …
… 后画出如下部分频率分布直方图.
后画出如下部分频率分布直方图.
科目:高中数学 来源:不详 题型:单选题
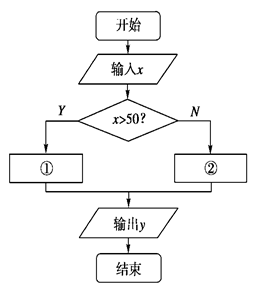
| A.y=0.85x | B.y=50×0.53+(x-50)×0.85 |
| C.y=0.53x | D.y=50×0.53+0.85x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
人数 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
件数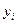 | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
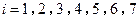 .
. (Ⅱ)求回归直线方程.(结果保留到小数点后两位)
(Ⅱ)求回归直线方程.(结果保留到小数点后两位) ,
, ,
,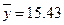 ,
,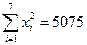 ,
, ,
,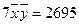 )
)
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如下图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如下图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.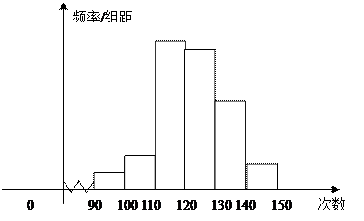
 在110以上(含110次)为达标,试估计该学校全体高一的学生达标的概率
在110以上(含110次)为达标,试估计该学校全体高一的学生达标的概率 等方面的关系,必须再从样本中按分层抽样方法抽出50人作进一步分析,则体能在[120,130)的这段应抽多少人?
等方面的关系,必须再从样本中按分层抽样方法抽出50人作进一步分析,则体能在[120,130)的这段应抽多少人?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 带来的便捷与舒适的同时,却不得不呼吸汽车排放的尾气”,汽车已是城市中碳排放量比较大的行业之一.某市为响应国家节能减排,更好地保护环境,决定将于
带来的便捷与舒适的同时,却不得不呼吸汽车排放的尾气”,汽车已是城市中碳排放量比较大的行业之一.某市为响应国家节能减排,更好地保护环境,决定将于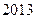 年起取消
年起取消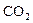 排放量超过
排放量超过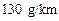 的
的 型新车挂牌.检测单位对目前该市保有量最大的甲类
型新车挂牌.检测单位对目前该市保有量最大的甲类 型品牌车随机抽取
型品牌车随机抽取 辆进行了
辆进行了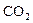 排放量检测,
排放量检测, 记录如下(单位:
记录如下(单位: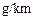 ).
).
 ,求
,求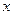 的值及样本标准差;
的值及样本标准差;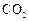 排放量的概率是多少?
排放量的概率是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
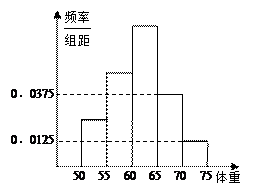

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的号码为16,则第四组抽取的号码
的号码为16,则第四组抽取的号码 为___________________.
为___________________.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
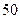 名学生。调査结果表明:在爱看课外书的
名学生。调査结果表明:在爱看课外书的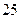 人中有
人中有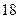 人作文水平好,另
人作文水平好,另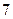 人作文水平一般;在不爱看课外书的
人作文水平一般;在不爱看课外书的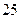 人中有
人中有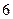 人作文水平好,另
人作文水平好,另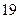 人作文水平一般.
人作文水平一般.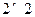 列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文
列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文 水平与爱看课外书有关系?
水平与爱看课外书有关系?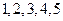 ,某
,某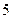 名爱看
名爱看 课外书且作文水平一般的学生也分别编号为
课外书且作文水平一般的学生也分别编号为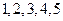 ,从这两组学生中各任选
,从这两组学生中各任选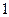 人进行学习交流,求被选取的两名学生的编号之和为
人进行学习交流,求被选取的两名学生的编号之和为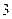 的倍数或
的倍数或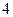 的倍数的概率.
的倍数的概率.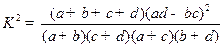
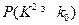 | 0. 10 | 0. 05 | 0. 025 | 0.010 | 0. 005 | 0. 001 |
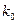 | 2. 706 | 3. 841 | 5. 024 | 6. 635 | 7. 879 | 10. 828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com