
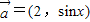 ,
, ,函数f(x)=
,函数f(x)=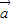 •
•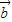 .
.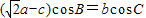 ,求f(A)的取值范围.
,求f(A)的取值范围.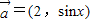 ,
,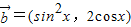 ,利用平面向量的数量积公式,我们可以求出函数f(x)=
,利用平面向量的数量积公式,我们可以求出函数f(x)=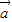 •
•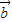 的解析式,并利用降幂公式(二倍角公式逆用),及辅助角公式,我们可将函数f(x)的解析式化为正弦型函数的形式,进而根据正弦型函数性质,求出f(x)的单调增区间;
的解析式,并利用降幂公式(二倍角公式逆用),及辅助角公式,我们可将函数f(x)的解析式化为正弦型函数的形式,进而根据正弦型函数性质,求出f(x)的单调增区间;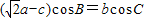 ,化为
,化为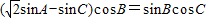 的形式,进而求出A的取值范围,结合(I)中所得的正弦型函数的性质,得到f(A)的取值范围.
的形式,进而求出A的取值范围,结合(I)中所得的正弦型函数的性质,得到f(A)的取值范围.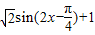 …(3分)
…(3分)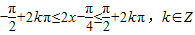 时,
时,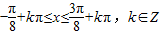 时,f(x)是单调递增.…(5分)
时,f(x)是单调递增.…(5分) …(6分)
…(6分)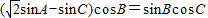 ,
,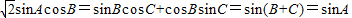
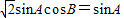 …(8分)
…(8分)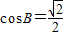 ,又∵0<B<π,∴
,又∵0<B<π,∴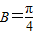 …(10分)
…(10分)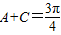 ,得:
,得: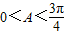 ,…(11分)
,…(11分)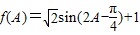 ,
,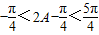
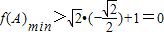 ,
,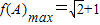
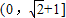 …(14分)
…(14分)

科目:高中数学 来源:2010-2011学年浙江省温州市十校联合体高三(上)期末数学试卷(理科)(解析版) 题型:解答题
 ,
,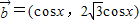 ,函数f(x)=
,函数f(x)=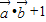 .
.查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高一(上)期末数学试卷(解析版) 题型:解答题
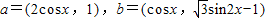 ,设函数f(x)=a•b,其中x∈R.
,设函数f(x)=a•b,其中x∈R.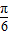 个单位得到g(x)的图象,求g(x)的解析式.
个单位得到g(x)的图象,求g(x)的解析式.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省苏州市高一(上)期末数学复习试卷3(解析版) 题型:解答题
 ,
,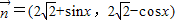 ,函数f(x)=
,函数f(x)= ,x∈R.
,x∈R.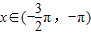 ,且f(x)=1,求
,且f(x)=1,求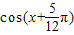 的值.
的值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省保定市新华中学高三摸底数学试卷(解析版) 题型:解答题
 ,
, ,函数f(x)=
,函数f(x)=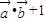 .
.查看答案和解析>>
科目:高中数学 来源:2011年浙江省杭州市萧山区高考数学模拟试卷02(文科)(解析版) 题型:解答题
 ,
, ,函数f(x)=
,函数f(x)= .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com