
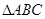 内有任意三点不共线的2006个点,加上A、B、C三个顶点,共2009个点,把这2009个点连线形成互不重叠的小三角形,则一共可以形成小三角形的个数为( )
内有任意三点不共线的2006个点,加上A、B、C三个顶点,共2009个点,把这2009个点连线形成互不重叠的小三角形,则一共可以形成小三角形的个数为( )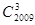 (B)4010 (C)4011 (D)4013
(B)4010 (C)4011 (D)4013

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源:不详 题型:填空题
 队中选出4人参
队中选出4人参查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
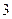 人坐在有八个座位的一排上,若每人的左右两边都要有空位,则不同的坐法的种数为几种?
人坐在有八个座位的一排上,若每人的左右两边都要有空位,则不同的坐法的种数为几种?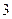 人站在共有
人站在共有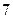 级的台阶上,若每级台阶最多站
级的台阶上,若每级台阶最多站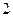 人,同一级台阶上
人,同一级台阶上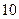 个保送大学的名额,分配给
个保送大学的名额,分配给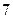 所学校,每校
所学校,每校 至少
至少 个名额,问名额分配的方法共有多少种?
个名额,问名额分配的方法共有多少种?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com