
【题目】某校学生会为了解该校学生对2017年全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类.已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数与女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(1)根据题意建立![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?
(2)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人进行回访,求这2人全是男生的概率.
参考公式和数据:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
【答案】(1)没有![]() 的把握认为男生与女生对两会的关注有差异;(2)
的把握认为男生与女生对两会的关注有差异;(2)![]() .
.
【解析】
(1)“比较关注”的学生中男生人数与女生人数之比为![]() ,构造方程求得
,构造方程求得![]() 列联表数据,依据公式计算得到
列联表数据,依据公式计算得到![]() 的观测值,可知无
的观测值,可知无![]() 的把握;(2)通过分层抽样确定抽取的男女生人数,再列举出所有可能的结果,根据古典概型得到结果.
的把握;(2)通过分层抽样确定抽取的男女生人数,再列举出所有可能的结果,根据古典概型得到结果.
(1)由这![]() 名学生中男生比女生多
名学生中男生比女生多![]() 人,可得男生人数为
人,可得男生人数为![]() ,女生人数为
,女生人数为![]() ,
,
设男生中“不太关注”的人数为![]() ,则男生中“比较关注”的人数为
,则男生中“比较关注”的人数为![]() ,
,
由“不太关注”的学生中男生比女生少![]() 人,可得女生中“不太关注”的人数为
人,可得女生中“不太关注”的人数为![]() ,
,
则女生中“比较关注”的人数为![]() ,
,
由“比较关注”的学生中男生人数与女生人数之比为![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
则![]() 列联表如下:
列联表如下:
比较关注 | 不太关注 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
则![]() 的观测值
的观测值![]() ,
,
所以没有![]() 的把握认为男生与女生对两会的关注有差异.
的把握认为男生与女生对两会的关注有差异.
(2)由题意得男生抽![]() 人、女生抽
人、女生抽![]() 人,
人,
记这![]() 名男生分别为
名男生分别为![]() ,
,![]() 名女生分别为
名女生分别为![]()
则所有的可能情况为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 种,其中
种,其中![]() 人全是男生的有
人全是男生的有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 种,
种,
故所求概率![]() .
.


科目:高中数学 来源: 题型:
【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高二年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高二年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 |
| 5 |
表2:女生
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | 3 |
|
(1)由表中统计数据填写下边![]() 列联表:
列联表:
男生 | 女生 | 总计 | |||||
优秀 | |||||||
非优秀 | 总计 |
(2)试采用独立性检验进行分析,能否在犯错误的概率不超过0.1的前提下认为“测评结果优秀与性别有关”.
参考数据与公式: ,其中
,其中![]() .
.
临界值表:
| 0.1 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 轴,直线
轴,直线![]() 交
交![]() 轴于
轴于![]() 点,
点,![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 的面积的最大值为1.
的面积的最大值为1.
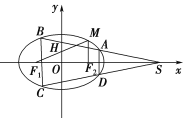
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条直线与椭圆
作两条直线与椭圆![]() 分别交于
分别交于![]() 且使
且使![]() 轴,如图,问四边形
轴,如图,问四边形![]() 的两条对角线的交点是否为定点?若是,求出定点的坐标;若不是,请说明理由.
的两条对角线的交点是否为定点?若是,求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20为市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:
甲校:58,66,71,58,67,72,82,92,83,86,67,59,86,72,78,59,68,69,73,81;
乙校:90,80,73,65,67,69,81,85,82,88,89,86,86,78,98,95,96,91,76,69,.
检查组将成绩分成了四个等级:成绩在区间![]() 的为
的为![]() 等,在区间
等,在区间![]() 的为
的为![]() 等,在区间
等,在区间![]() 的为
的为![]() 等,在区间
等,在区间![]() 为
为![]() 等.
等.

(1)请用茎叶图表示上面的数据,并通过观察茎叶图,对两所学校办学的社会满意度进行比较,写出两个统计结论;
(2)估计哪所学校的市民的评分等级为![]() 级或
级或![]() 级的概率大,说明理由.
级的概率大,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点![]() 的两条互相垂直的直线与抛物线
的两条互相垂直的直线与抛物线![]() 相交于不同于原点的两点
相交于不同于原点的两点![]() ,且
,且![]() 轴,
轴,![]() 的面积为16.
的面积为16.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)已知点![]() ,
,![]() ,
,![]() 为抛物线
为抛物线![]() 上不同的三点,若
上不同的三点,若![]() ,试问:直线
,试问:直线![]() 是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下结论:
①命题“若![]() ,则
,则![]() ”的逆否命题“若
”的逆否命题“若![]() ,则
,则![]() ”;
”;
②“![]() ”是“
”是“![]() ”的充分条件;
”的充分条件;
③命题“若![]() ,则方程
,则方程![]() 有实根”的逆命题为真命题;
有实根”的逆命题为真命题;
④命题“若![]() ,则
,则![]() 且
且![]() ”的否命题是真命题.
”的否命题是真命题.
其中错误的是__________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取1名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在
使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在![]() 的概率;
的概率;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com