
分析 根据函数奇偶性的性质求出当x<0的解析式,讨论x>0,x<0,x=0,解不等式即可.
解答 解:若x<0,则-x>0,
∵当x>0时,f(x)=2x-3,
∴当-x>0时,f(-x)=2-x-3,
∵f(x)是定义在R上的奇函数,
∴f(-x)=2-x-3=-f(x),
则f(x)=-2-x+3,x<0,
当x>0时,不等式f(x)<-5等价为2x-3<-5即2x<-2,无解,不成立;
当x<0时,不等式f(x)<-5等价为-2-x+3<-5即2-x>8,
得-x>3,即x<-3;
当x=0时,f(0)=0,不等式f(x)<-5不成立,
综上,不等式的解为x<-3.
故不等式的解集为(-∞,-3).
故答案为(-∞,-3).
点评 本题主要考查不等式的解集的求解,根据函数奇偶性的性质求出函数的解析式是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.
如图,四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{3}{4}$)∪(-$\frac{1}{4}$,+∞) | B. | (-∞,-$\frac{3}{4}$) | C. | (-$\frac{1}{4}$,+∞) | D. | (-$\frac{3}{4}$,-$\frac{1}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
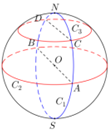 如图,N、S是球O直径的两个端点,圆C1是经过N和S点的大圆,圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆,圆C1和C2交于点A、B,圆C1和C3交于点C、D,设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长,则a、b、c的大小关系为( )
如图,N、S是球O直径的两个端点,圆C1是经过N和S点的大圆,圆C2和圆C3分别是所在平面与NS垂直的大圆和小圆,圆C1和C2交于点A、B,圆C1和C3交于点C、D,设a、b、c分别表示圆C1上劣弧CND的弧长、圆C2上半圆弧AB的弧长、圆C3上半圆弧CD的弧长,则a、b、c的大小关系为( )| A. | b>a=c | B. | b=c>a | C. | b>a>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:解答题
已知函数
(1)判断 的奇偶性;
的奇偶性;
(2)若 ,函数
,函数 在区间
在区间 上为减函数,求实数a的取值范围.
上为减函数,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com