
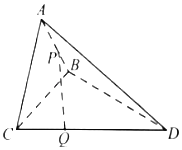
【题目】如图,在三棱锥A﹣BCD中,平面ABC⊥平面BCD,△BAC与BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°的角,则线段PA长的取值范围是( )
A.(0,![]() )B.[0,
)B.[0,![]() ]C.(
]C.(![]() ,
,![]() )D.(
)D.(![]() ,
,![]() )
)
科目:高中数学 来源: 题型:
【题目】在中美组织的暑假中学生交流会结束时,中方组织者将孙悟空、猪八戒、沙和尚、唐三藏、白龙马的彩色陶俑各一个送给来中国参观的美国中学生汤姆、杰克、索菲娅,每个人至少一个,且猪八戒的彩色陶俑不能送给索菲娅,则不同的送法种数为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:![]() 与曲线C:
与曲线C:![]() (
(![]() ,
,![]() )交于不同的两点A,B,O为坐标原点.
)交于不同的两点A,B,O为坐标原点.
(1)若![]() ,
,![]() ,求证:曲线C是一个圆;
,求证:曲线C是一个圆;
(2)若曲线C过![]() 、
、![]() ,是否存在一定点Q,使得
,是否存在一定点Q,使得![]() 为定值?若存在,求出定点Q和定值;若不存在,请说明理由.
为定值?若存在,求出定点Q和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量AQI指数是反映空气质量状况指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI指数值 |
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图所示的是某市11月1日至20日AQI指数变化的折线图:
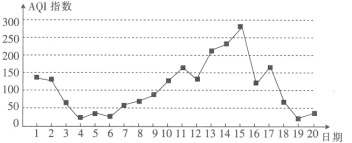
下列说法不正确的是( )
A.这![]() 天中空气质量为轻度污染的天数占
天中空气质量为轻度污染的天数占![]()
B.这![]() 天中空气质量为优和良的天数为
天中空气质量为优和良的天数为![]() 天
天
C.这![]() 天中AQI指数值的中位数略低于
天中AQI指数值的中位数略低于![]()
D.总体来说,该市11月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月,教育部《关于在部分高校开展基础学科招生改革试点工作的意见》印发,自2020年起,在部分高校开展基础学科招生改革试点(也称“强基计划”).强基计划聚焦高端芯片与软件智能科技新材料先进制造和国家安全等关键领域以及国家人才紧缺的人文社会科学领域,选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生.新材料产业是重要的战略性新兴产业,下图是我国2011-2019年中国新材料产业市场规模及增长趋势图.其中柱状图表示新材料产业市场规模(单位:万亿元),折线图表示新材料产业市场规模年增长率(![]() ).
).
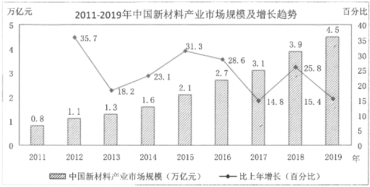
(1)求2015年至2019年这5年的新材料产业市场规模的平均数;
(2)从2012年至2019年中随机挑选一年,求该年新材料产业市场规模较上一年的年增加量不少于6000亿元的概率;
(3)由图判断,从哪年开始连续三年的新材料产业市场规模年增长率的方差最大.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin 3x-![]() cos 3x+1的图象向左平移
cos 3x+1的图象向左平移![]() 个单位长度,得到函数g(x)的图象,给出下列关于g(x)的结论:
个单位长度,得到函数g(x)的图象,给出下列关于g(x)的结论:
①它的图象关于直线x=![]() 对称;
对称;
②它的最小正周期为![]() ;
;
③它的图象关于点(![]() ,1)对称;
,1)对称;
④它在[![]() ]上单调递增.
]上单调递增.
其中所有正确结论的编号是( )
A.①②B.②③C.①②④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解高一年级学生学习数学的状态,从期中考试成绩中随机抽取50名学生的数学成绩,按成绩分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
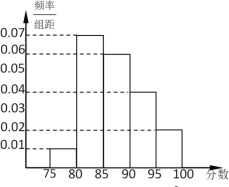
(1)由频率分布直方图,估计这50名学生数学成绩的中位数和平均数(保留到0.01);
(2)该校高一年级共有1000名学生,若本次考试成绩90分以上(含90分)为“优秀”等次,则根据频率分布直方图估计该校高一学生数学成绩达到“优秀”等次的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明.下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用![]() ,化简,得
,化简,得![]() .设勾股形中勾股比为
.设勾股形中勾股比为![]() ,若向弦图内随机抛掷
,若向弦图内随机抛掷![]() 颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com