
 sin30°=
sin30°= ,可得这个常数的值.
,可得这个常数的值. .证明方法一:直接利用两角差的余弦公式代入等式的左边,化简可得结果.
.证明方法一:直接利用两角差的余弦公式代入等式的左边,化简可得结果. +
+ -sinα(cos30°cosα+sin30°sinα),即 1-
-sinα(cos30°cosα+sin30°sinα),即 1- +
+ cos2α+
cos2α+ sin2α
sin2α sin2α-
sin2α- ,化简可得结果.
,化简可得结果. sin30°=
sin30°= ,故 这个常数为
,故 这个常数为 .
. .
. -sinα(cos30°cosα+sin30°sinα)
-sinα(cos30°cosα+sin30°sinα) cos2α+
cos2α+ sin2α+
sin2α+ sinαcosα-
sinαcosα- sinαcosα-
sinαcosα- sin2α=
sin2α= sin2α+
sin2α+ cos2α=
cos2α= .
. +
+ -sinα(cos30°cosα+sin30°sinα)
-sinα(cos30°cosα+sin30°sinα) +
+ (cos60°cos2α+sin60°sin2α)-
(cos60°cos2α+sin60°sin2α)-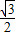 sin2α-
sin2α- sin2α
sin2α +
+ cos2α+
cos2α+ sin2α-
sin2α- sin2α-
sin2α- =1-
=1- -
- +
+ =
= .
.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高三上学期第一次月考文科数学试卷(解析版) 题型:解答题
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数 .
.
① ;
;
② ;
;
③ ;
;
④ ;
;
⑤ .
.
(1)从上述五个式子中选择一个,求出常数 ;
;
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com