
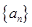 的前
的前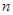 项和
项和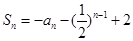 (
(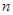 为正整数)
为正整数)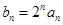 ,求证数列
,求证数列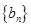 是等差数列,并求数列
是等差数列,并求数列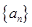 的通项公式;
的通项公式;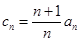 ,
,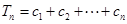 ,试比较
,试比较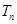 与
与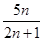 的大小,并予以证明
的大小,并予以证明 的前
的前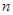 项和表达式,先根据
项和表达式,先根据 求数列
求数列 的通项
的通项 的递推关系式,再求数列
的递推关系式,再求数列 是等差数列,根据等差数列
是等差数列,根据等差数列 的通项求数列
的通项求数列 的通项;(2)由(1)所求数列
的通项;(2)由(1)所求数列 的通项
的通项 先得
先得 ,再利用错位相减法求
,再利用错位相减法求 得表达式,再把
得表达式,再把 与
与 作差比较大小,可利用数学归纳法证明
作差比较大小,可利用数学归纳法证明 中,令n=1,可得
中,令n=1,可得 ,即
,即
 时,
时, ,
,

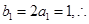 数列
数列 是首项和公差均为1的等差数列
是首项和公差均为1的等差数列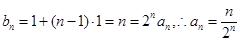
 ,所以
,所以




 的大小关系等价于比较
的大小关系等价于比较 的大小
的大小
 证明如下:
证明如下: 时,
时, ,
, 时猜想成立,
时猜想成立, 的正整数,都有
的正整数,都有
 时
时 ,
,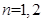 时,
时, ;当
;当 时
时
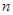 项和;2、错位相减法求和;3、作差比较法
项和;2、错位相减法求和;3、作差比较法

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com