练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知圆C1：与圆C2：相交于A、B两点，

    (1)求公共弦AB所在的直线方程；

    (2)求圆心在直线上，且经过A、B两点的圆的方程．

    【答案】(1)x－2y＋4＝0.(2)⊙M：(x＋3)2＋(y－3)2＝10.

    【解析】

    试题分析：（1）由两圆方程相减即得公共弦AB所在的直线方程；（2）求出过的直线与直线y=-x的交点，可得圆心坐标，求出圆心到AB的距离，可得半径，从而可得圆的方程

    试题解析：（1）x－2y＋4＝0．

    （2）由（1）得x＝2y－4，代入x2＋y2＋2x＋2y－8＝0中得：y2－2y＝0．

    ∴或，即A（－4，0），B（0，2），

    又圆心在直线y＝－x上，设圆心为M（x，－x），

    则|MA|＝|MB|，解得M（－3，3），

    ∴⊙M：（x＋3）2＋（y－3）2＝10．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足 ，则{an}的前50项的和为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足 ，an+1bn=bn+1an+bn ， 且 （n∈N*），则数列{an}的前2n项和S2n取最大值时，n= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l的参数方程为 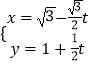（t为参数），以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，圆C的极坐标方程为 ．
    （1）求圆C的直角坐标方程；
    （2）若P（x，y）是直线l与圆面 的公共点，求 的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设 ， 是非零向量，则“ ， 共线”是“| |+| |=| + |”的（ ）
    A.充分而不必要条件
    B.必要而不充分条件
    C.充分必要条件
    D.既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直线l经过两直线l1:2x-y+4=0与l2:x-y+5=0的交点,且与直线x-2y-6=0垂直.

    (1)求直线l的方程.

    (2)若点P(a,1)到直线l的距离为,求实数a的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者．从符合条件的500名志愿者中随机抽取100名志愿者，其年龄频率分布直方图如图所示，

    （1）求图中的值并根据频率分布直方图估计这500名志愿者中年龄在岁的人数；

    （2）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动，再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人．记这3名志愿者中“年龄低于35岁”的人数为，求的分布列及均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在底面是直角梯形的四棱锥S-ABCD中，面.

    (1)求四棱锥S-ABCD的体积;

    (2)求证：面

    (3)求SC与底面ABCD所成角的正切值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分13分）在四棱锥中， ,

    ， 平面，直线PC与平面ABCD所成角为， ．

    （Ⅰ）求四棱锥的体积；

    （Ⅱ）若为的中点，求证：平面 平面．

    查看答案和解析>>

    同步练习册答案