
【题目】已知直线l过点P(3,6)且与x,y轴的正半轴分别交于A、B两点,O是坐标原点,则当|OA|+|OB|取得最小值时的直线方程是(用一般式表示)
【答案】![]() x+y﹣6﹣3
x+y﹣6﹣3 ![]() =0
=0
【解析】解:由题意可得:设直线的斜率为k,因为直线l与x轴的正半轴,y轴的正半轴分别交于A、B两点,
所以得到k<0.
则直线l的方程为:y﹣6=k(x﹣3),整理可得:kx﹣y+6﹣3k=0,
令x=0,得y=6﹣3k,所以B(0,6﹣3k);
令y=0,得到x=3﹣ ![]() ,所以A(3﹣
,所以A(3﹣ ![]() ,0),
,0),
所以|OA|+|OB|=6﹣3k+3﹣ ![]() =9+(﹣3k)+(﹣
=9+(﹣3k)+(﹣ ![]() ),
),
因为k<0,则|OA|+|OB|=9+(﹣3k)+(﹣ ![]() )≥9+6
)≥9+6 ![]() ,
,
当且仅当﹣3k=﹣ ![]() ,即k=﹣
,即k=﹣ ![]() 时“=”成立,
时“=”成立,
所以直线l的方程为: ![]() x+y﹣6﹣3
x+y﹣6﹣3 ![]() =0,
=0,
所以答案是: ![]() x+y﹣6﹣3
x+y﹣6﹣3 ![]() =0.
=0.
【考点精析】关于本题考查的一般式方程,需要了解直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0)才能得出正确答案.
(A,B不同时为0)才能得出正确答案.


科目:高中数学 来源: 题型:
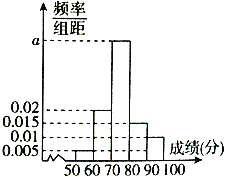
【题目】为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示.成绩落在[70,80)中的人数为20.
男生 | 女生 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(Ⅰ)求a和n的值;
(Ⅱ)根据样本估计总体的思想,估计该校高二学生物理成绩的平均数![]() 和中位数m;
和中位数m;
(Ⅲ)成绩在80分以上(含80分)为优秀,样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,完成2×2列联表,并判断是否有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:K2=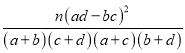 .
.
P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
k | 0.455 | 3.841 | 5.024 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,已知四边形![]() 是由直角△
是由直角△![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]()
![]() .且点
.且点![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() 现将△
现将△![]() 沿
沿![]() 进行翻折,使得二面角
进行翻折,使得二面角![]()
![]() 的大小为
的大小为![]() ,得到图形如图(2)所示,连接
,得到图形如图(2)所示,连接![]() ,点
,点![]() 分别在线段
分别在线段![]() 上.
上.


(1)证明: ![]() ;
;
(2)若三棱锥![]() 的体积为四棱锥
的体积为四棱锥![]() 体积的
体积的![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是空间两条直线,
是空间两条直线, ![]() 是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )
A. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
D. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
A.9.4,0.484
B.9.4,0.016
C.9.5,0.04
D.9.5,0.016
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解初三女生身高情况,某中学对初三女生身高情况进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合 计 | M | N |
(1)求出表中m,n,M,N所表示的数分别是多少?
(2)画出频率分布直方图;
(3)全体女生中身高在哪组范围内的人数最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]以平面直角坐标系原点为极点,x轴正半轴为极轴,建立极坐标系,两种坐标系中取相同长度单位,已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,( ![]() 为参数,且
为参数,且![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求![]() 的极坐标方程与
的极坐标方程与![]() 的直角坐标方程;
的直角坐标方程;
(2))若P是![]() 上任意一点,过点P的直线
上任意一点,过点P的直线![]() 交
交![]() 于点M,N,求
于点M,N,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张老师开车上班,有路线①与路线②两条路线可供选择. 路线①:沿途有![]() 两处独立运行的交通信号灯,且两处遇到绿灯的概率依次为
两处独立运行的交通信号灯,且两处遇到绿灯的概率依次为![]() ,若
,若![]() 处遇红灯或黄灯,则导致延误时间2分钟;若
处遇红灯或黄灯,则导致延误时间2分钟;若![]() 处遇红灯或黄灯,则导致延误时间3分钟;若两处都遇绿灯,则全程所花时间为20分钟.
处遇红灯或黄灯,则导致延误时间3分钟;若两处都遇绿灯,则全程所花时间为20分钟.
路线②:沿途有![]() 两处独立运行的交通信号灯,且两处遇到绿灯的概率依次为
两处独立运行的交通信号灯,且两处遇到绿灯的概率依次为![]() ,若
,若![]() 处遇红灯或黄灯,则导致延误时间8分钟;若
处遇红灯或黄灯,则导致延误时间8分钟;若![]() 处遇红灯或黄灯,则导致延误时间5分钟;若两处都遇绿灯,则全程所花时间为15分钟.
处遇红灯或黄灯,则导致延误时间5分钟;若两处都遇绿灯,则全程所花时间为15分钟.
(1)若张老师选择路线①,求他20分钟能到校的概率;
(2)为使张老师日常上班途中所花时间较少,你建议张老师选择哪条路线?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com