
【题目】如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设 ![]() ,
, ![]() ,则得到函数y=f(x).
,则得到函数y=f(x). 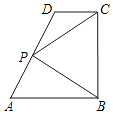
(Ⅰ)求f(1)的值;
(Ⅱ)对于任意a∈(0,+∞),求函数f(x)的最大值.
【答案】解:(1)如图所示,建立直角坐标系.
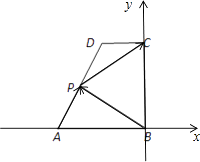
∵在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),
∴B(0,0),A(﹣2,0),D(﹣1,a),C(0,a).
∵ ![]() =x
=x ![]() ,(0≤x≤1).
,(0≤x≤1).
∴ ![]() =
= ![]() +x
+x ![]() =(﹣2,0)+x(1,a)=(x﹣2,xa),
=(﹣2,0)+x(1,a)=(x﹣2,xa),
∴ ![]() =
= ![]() ﹣
﹣ ![]() =(0,a)﹣(x﹣2,xa)=(2﹣x,a﹣xa)
=(0,a)﹣(x﹣2,xa)=(2﹣x,a﹣xa)
∴y=f(x)= ![]()
![]() =(2﹣x,﹣xa)(2﹣x,a﹣xa)
=(2﹣x,﹣xa)(2﹣x,a﹣xa)
=(2﹣x)2﹣ax(a﹣xa)
=(a2+1)x2﹣(4+a2)x+4.
∴f(1)=a2+1﹣(4+a2)+4=1
(Ⅱ)由y=f(x)=(a2+1)x2﹣(4+a2)x+4.
可知:对称轴x0= 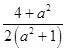 .
.
当0<a≤ ![]() 时,1<x0,∴函数f(x)在[0,1]单调递减,因此当x=0时,函数f(x)取得最大值4.
时,1<x0,∴函数f(x)在[0,1]单调递减,因此当x=0时,函数f(x)取得最大值4.
当a> ![]() 时,0<x0<1,函数f(x)在[0,x0)单调递减,在(x0,1]上单调递增.
时,0<x0<1,函数f(x)在[0,x0)单调递减,在(x0,1]上单调递增.
又f(0)=4,f(1)=1,
∴f(x)max=f(0)=4.
综上所述函数f(x)的最大值为4
【解析】(Ⅰ)画出图形,建立直角坐标系,即得y=f(x)的解析式,代值计算即可(Ⅱ)通过分类讨论,利用二次函数的单调性即可判断出.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】下列命题中 ①若loga3>logb3,则a>b;
②函数f(x)=x2﹣2x+3,x∈[0,+∞)的值域为[2,+∞);
③设g(x)是定义在区间[a,b]上的连续函数.若g(a)=g(b)>0,则函数g(x)无零点;
④函数 ![]() 既是奇函数又是减函数.
既是奇函数又是减函数.
其中正确的命题有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1﹣ ![]() 为定义在R上的奇函数.
为定义在R上的奇函数.
(1)试判断函数的单调性,并用定义加以证明;
(2)若关于x的方程f(x)=m在[﹣1,1]上有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个平面垂直,下列命题: ①一个平面内的已知直线必垂直于另一个平面内的任意一条直线.
②一个平面内的已知直线必垂直于另一个平面内的无数条直线.
③一个平面内的任一条直线必垂直于另一个平面.
④一个平面内垂直于交线的直线与另一个平面垂直.
其中正确命题的个数是( )
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD中平面PAB⊥平面ABCD,底面ABCD是正方形.点M是棱PC的中点 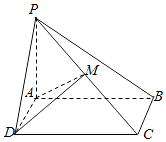
(1)记平面ADM与平面PBC的交线是l,试判断直线l与BC的位置关系,并加以证明.
(2)若 ![]() ,求证PB⊥平面ADM,并求直线PC与平面ADM所成角的正弦值.
,求证PB⊥平面ADM,并求直线PC与平面ADM所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,其前n项和为Sn , 且满足an= ![]() (n≥2)
(n≥2)
(1)求Sn;
(2)证明:当n≥2时,S1+ ![]() S2+
S2+ ![]() S3+…+
S3+…+ ![]() Sn<
Sn< ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com