Question

(本小题满分13分)
已知数列{a_n}的前n项和为S_n，S_n=2-(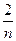+1)a_n(n≥1)．
（1）求证：数列{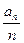}是等比数列；
（2）设数列{2ⁿa_n}的前n项和为T_n，A_n=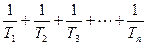.试比较A_n与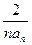的大小。

Answer 1

解：（1）由a₁=S₁=2-3a₁得a₁=，                               1分
由S_n=2-(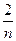+1)a_n得S_n-1=2-(+1)a_n-1，
于是a_n=S_n- S_n-1=(+1)a_n-1-(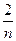+1)a_n，
整理得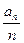=×（n≥2）,                                    4分
所以数列{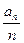}是首项及公比均为的等比数列.                       5分
（2）由（Ⅰ）得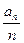=×=.                            6分
于是2ⁿa_n=n，T_n=1+2+3+…+n=，                           7分
_，
A_n=2[（1-）+（-）+…+=2（1-）=.
9分
又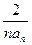=,问题转化为比较与的大小,即与的大小.
设f(n)= ，g(n)=.
∵f(n+1)-f(n)=，当n≥3时, f(n+1)-f(n)>0,
∴当n≥3时f(n)单调递增，                                        11分
∴当n≥4时，f(n) ≥f(4)=1，而g(n)<1, ∴当n≥4时f(n) >g(n)，
经检验n=1,2,3时，仍有f(n) ≥g(n)，
因此，对任意正整数n，都有f(n) >g(n),
即A_n <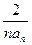.                                                    13分

解析