
【题目】某企业对设备进行升级改造,现从设备改造前后生产的大量产品中各抽取了100件产品作为样本,检测一项质量指标值,该项质量指标值落在区间![]() 内的产品视为合格品,否则视为不合格品,如图是设备改造前样本的频率分布直方图,下表是设备改造后样本的频数分布表.
内的产品视为合格品,否则视为不合格品,如图是设备改造前样本的频率分布直方图,下表是设备改造后样本的频数分布表.
图:设备改造前样本的频率分布直方图
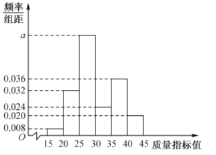
表:设备改造后样本的频率分布表
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 18 | 48 | 14 | 16 | 2 |
(1)求图中实数![]() 的值;
的值;
(2)企业将不合格品全部销毁后,对合格品进行等级细分,质量指标值落在区间![]() 内的定为一等品,每件售价240元;质量指标值落在区间
内的定为一等品,每件售价240元;质量指标值落在区间![]() 或
或![]() 内的定为二等品,每件售价180元;其他的合格品定为三等品,每件售价120元,根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.若有一名顾客随机购买两件产品支付的费用为
内的定为二等品,每件售价180元;其他的合格品定为三等品,每件售价120元,根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.若有一名顾客随机购买两件产品支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知平面向量![]() ,
,![]() 满足:|
满足:|![]() |=2,|
|=2,|![]() |=1.
|=1.
(1)若(![]() 2
2![]() )(
)(![]() )=1,求
)=1,求![]()
![]() 的值;
的值;
(2)设向量![]() ,
,![]() 的夹角为θ.若存在t∈R,使得
的夹角为θ.若存在t∈R,使得![]() ,求cosθ的取值范围.
,求cosθ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=(-x2+ax)ex(x∈R).
(1)当a=2时,求函数f(x)的单调区间;
(2)若函数f(x)在(-1,1)上单调递增,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】虚拟现实(![]() )技术被认为是经济发展的新增长点,某地区引进
)技术被认为是经济发展的新增长点,某地区引进![]() 技术后,
技术后,![]() 市场收入(包含软件收入和硬件收入)逐年翻一番,据统计该地区
市场收入(包含软件收入和硬件收入)逐年翻一番,据统计该地区![]() 市场收入情况如图所示,则下列说法错误的是( )
市场收入情况如图所示,则下列说法错误的是( )
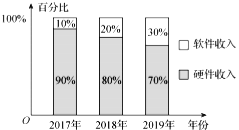
A.该地区2019年的![]() 市场总收入是2017年的4倍
市场总收入是2017年的4倍
B.该地区2019年的![]() 硬件收入比2017年和2018年的硬件收入总和还要多
硬件收入比2017年和2018年的硬件收入总和还要多
C.该地区2019年的![]() 软件收入是2018年的软件收入的3倍
软件收入是2018年的软件收入的3倍
D.该地区2019年的![]() 软件收入是2017年的软件收入的6倍
软件收入是2017年的软件收入的6倍
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com