
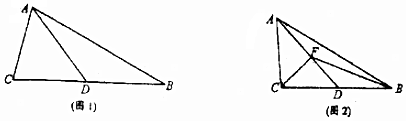
分析 (1)延长AD到A1使得AD=DA1,连接CA1,A1B,证明四边形ACA1B是平行四边形,即可证明:$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$);
(2)运用向量加法三角形法则,以及向量垂直的性质:数量积为0,斜率的平方即为模的平方,即可得到所求常数;
(3)设|$\overrightarrow{AF}$|=x,则|$\overrightarrow{FD}$|=$\sqrt{2}$-x(0≤x≤$\sqrt{2}$),运用向量共线和向量数量积的定义,可得$\overrightarrow{AF}$•($\overrightarrow{FB}$+$\overrightarrow{FC}$)=2x($\sqrt{2}$-x),利用基本不等式,可得所求的范围.
解答 (1)证明:延长AD到A1使得AD=DA1,连接CA1,A1B,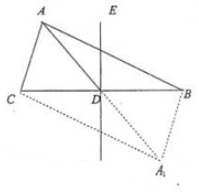
∵D是BC的中点,
∴四边形ACA1B是平行四边形,
∴$\overrightarrow{A{A}_{1}}$=$\overrightarrow{AB}$+$\overrightarrow{AC}$,
∵$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{A{A}_{1}}$,
则$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$);
(2)证明:∵$\overrightarrow{AE}$=$\overrightarrow{AD}$+$\overrightarrow{DE}$,
∴$\overrightarrow{AE}$•($\overrightarrow{AB}$-$\overrightarrow{AC}$)=($\overrightarrow{AD}$+$\overrightarrow{DE}$)•($\overrightarrow{AB}$-$\overrightarrow{AC}$)
=$\overrightarrow{AD}$•$\overrightarrow{CB}$+$\overrightarrow{DE}$•$\overrightarrow{CB}$,
∵DE⊥BC,∴$\overrightarrow{DE}$•$\overrightarrow{CB}$=0,
∵$\overrightarrow{AD}$•$\overrightarrow{CB}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)•($\overrightarrow{AB}$-$\overrightarrow{AC}$)
=$\frac{1}{2}$($\overrightarrow{AB}$2-$\overrightarrow{AC}$2)=$\frac{1}{2}$×(4-1)=$\frac{3}{2}$,
∴$\overrightarrow{AE}$•($\overrightarrow{AB}$-$\overrightarrow{AC}$)=$\frac{3}{2}$;
(3)解:△ABC中,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=1,cosA=$\frac{3}{4}$,$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),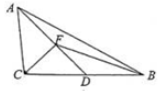
∴|$\overrightarrow{AD}$|=$\frac{1}{2}$$\sqrt{{\overrightarrow{AB}}^{2}+{\overrightarrow{AC}}^{2}+2\overrightarrow{AB}•\overrightarrow{AC}}$=$\frac{1}{2}$$\sqrt{4+2×2×1×\frac{3}{4}+1}$=$\sqrt{2}$,
同理$\overrightarrow{FB}$+$\overrightarrow{FC}$=2$\overrightarrow{FD}$,
∴$\overrightarrow{AF}$•($\overrightarrow{FB}$+$\overrightarrow{FC}$)=$\overrightarrow{AF}$•2$\overrightarrow{FD}$=2|$\overrightarrow{AF}$|•|$\overrightarrow{FD}$|,
设|$\overrightarrow{AF}$|=x,则|$\overrightarrow{FD}$|=$\sqrt{2}$-x(0≤x≤$\sqrt{2}$),
∴$\overrightarrow{AF}$•($\overrightarrow{FB}$+$\overrightarrow{FC}$)=2x($\sqrt{2}$-x)≤2($\frac{x+\sqrt{2}-x}{2}$)2=1,
当且仅当x=$\frac{\sqrt{2}}{2}$时取等号,
∴$\overrightarrow{AF}$•($\overrightarrow{FB}$+$\overrightarrow{FC}$)∈(0,1].
点评 本题考查平面向量知识的运用,考查向量数量积的计算,考查学生分析解决问题的能力,属于中档题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| x | x1 | x2 | x3 | x4 | 5 |
| y | 2.5 | 4.6 | 5.4 | n | 7.5 |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 4 | 5 | 6 | 7 |
| y | 8.2 | 7.8 | 6.6 | 5.4 |
| A. | -0.96 | B. | -0.94 | C. | -0.92 | D. | -0.98 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,-1] | B. | (-∞,-1] | C. | [1,2] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参加运动 | 不参加运动 | 合计 | |
| 男大学生 | 20 | 8 | 28 |
| 女大学生 | 12 | 16 | 28 |
| 合计 | 32 | 24 | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com