
【题目】已知函数f(x)=|x+1|. (I)求不等式f(x)<|2x+1|﹣1的解集M;
(Ⅱ)设a,b∈M,证明:f(ab)>f(a)﹣f(﹣b).
【答案】解:(I)不等式f(x)<|2x+1|﹣1,即|x+1|<|2x+1|﹣1, ∴ ![]() ①,或
①,或 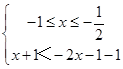 ②,或
②,或 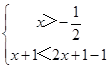 ③.
③.
解①求得x<﹣1;解②求得x∈;解③求得x>1.
故要求的不等式的解集M={x|x<﹣1或 x>1}.
(Ⅱ)证明:设a,b∈M,∴|a+1|>0,|b|﹣1>0,
则 f(ab)=|ab+1|,f(a)﹣f(﹣b)=|a+1|﹣|﹣b+1|.
∴f(ab)﹣[f(a)﹣f(﹣b)]=f(ab)+f(﹣b)﹣f(a)=|ab+1|+|1﹣b|﹣|a+1|
=|ab+1|+|b﹣1|﹣|a+1|≥|ab+1+b﹣1|﹣|a+1|=|b(a+1)|﹣|a+1|
=|b||a+1|﹣|a+1|=|a+1|(|b|﹣1|)>0,
故f(ab)>f(a)﹣f(﹣b)成立
【解析】(I)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.(Ⅱ)由题意可得|a+1|>0,|b|﹣1>0,化简f(ab)﹣[f(a)﹣f(﹣b)]为|a+1|(|b|﹣1|)>0,从而证得不等式成立.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】已知长方形ABCD如图1中,AD= ![]() ,AB=2,E为AB中点,将△ADE沿DE折起到△PDE,所得四棱锥P﹣BCDE如图2所示.
,AB=2,E为AB中点,将△ADE沿DE折起到△PDE,所得四棱锥P﹣BCDE如图2所示.
(Ⅰ)若点M为PC中点,求证:BM∥平面PDE;
(Ⅱ)当平面PDE⊥平面BCDE时,求三棱锥E﹣PCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,解不等式
,解不等式![]() ;
;
(Ⅱ)设![]() 是函数
是函数![]() 的四个不同的零点,问是否存在实数
的四个不同的零点,问是否存在实数![]() ,使得其中三个零点成等差数列?若存在,求出所有
,使得其中三个零点成等差数列?若存在,求出所有![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD﹣A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1= ![]() ,∠BAD=120°.
,∠BAD=120°.
(Ⅰ)求异面直线A1B与AC1所成角的余弦值;
(Ⅱ)求二面角B﹣A1D﹣A的正弦值.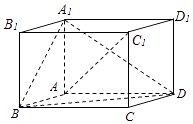
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com