
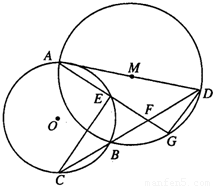
 如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.
如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.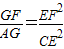 .
. ,
, ,
, .
.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
 如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.
如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为BD中点,连接AG分别交⊙O、BD于点E、F连接CE.| GF |
| AG |
| EF2 |
| CE2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BD的中点,连接AG分别交⊙O、BD于点E、F,连接CE.
如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BD的中点,连接AG分别交⊙O、BD于点E、F,连接CE.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•长春一模)请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
(2013•长春一模)请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分. |
| BD |
| GF |
| AG |
| EF2 |
| CE2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年海南省等4校联考理科数学试卷(解析版) 题型:解答题
如图,已知⊙O和⊙M相交于A.B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BD中点,连结AG分别交⊙O.BD于点E.F连结CE。
(Ⅰ)求证: ;
;
(Ⅱ)求证:

查看答案和解析>>
科目:高中数学 来源:2011-2012学年辽宁省沈阳四校高三上学期12月月考理科数学试卷 题型:解答题
选修4-1:几何证明选讲
如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧 的中点,连结AG分别交⊙O、BD于点E、F,连结CE.
的中点,连结AG分别交⊙O、BD于点E、F,连结CE.
(Ⅰ)求证: 为⊙O的直径。
为⊙O的直径。
(Ⅱ)求证: ;
;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com