
【题目】设椭圆![]() 的一个顶点与抛物线
的一个顶点与抛物线![]() 的焦点重合,
的焦点重合,![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,其离心率
的左、右焦点,其离心率![]() 椭圆
椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
(1)求出抛物线![]() 的焦点坐标可得出
的焦点坐标可得出![]() ,再结合离心率求出
,再结合离心率求出![]() 的值,由此可得出椭圆
的值,由此可得出椭圆![]() 的方程;
的方程;
(2)分直线![]() 的斜率是否存在进行分类讨论,在直线
的斜率是否存在进行分类讨论,在直线![]() 的斜率不存在时,求出
的斜率不存在时,求出![]() 、
、![]() 两点的坐标,验证
两点的坐标,验证![]() 是否成立;在直线
是否成立;在直线![]() 的斜率存在时,可设直线
的斜率存在时,可设直线![]() 的方程为
的方程为![]() ,并设点
,并设点![]() 、
、![]() ,将直线
,将直线![]() 与椭圆
与椭圆![]() 的方程联立,并列出韦达定理,结合平面向量数量积的坐标运算得出关于
的方程联立,并列出韦达定理,结合平面向量数量积的坐标运算得出关于![]() 的方程,解出即可.
的方程,解出即可.
(1)由抛物线![]() 的焦点为
的焦点为![]() ,则知
,则知![]() ,
,
又结合![]() ,
,![]() ,解得
,解得![]() ,故椭圆方程为
,故椭圆方程为![]() ;
;
(2)若直线![]() 不存在,可得
不存在,可得 ,
,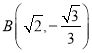 ,不满足
,不满足![]() ;
;
故直线斜率必然存在,由椭圆右焦点![]() ,可设直线
,可设直线![]() 为
为![]() ,
,
记直线![]() 与椭圆的交点
与椭圆的交点![]() 、
、![]() ,
,
由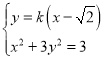 ,消去
,消去![]() 整理得到
整理得到![]() .
.
由题意可知![]() 恒成立,且有
恒成立,且有![]() ,
,![]() .
.
那么![]()

则![]() ,解得
,解得![]() .
.
因此,直线![]() 的方程为
的方程为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】至![]() 年底,我国发明专利申请量已经连续
年底,我国发明专利申请量已经连续![]() 年位居世界首位,下表是我国
年位居世界首位,下表是我国![]() 年至
年至![]() 年发明专利申请量以及相关数据.
年发明专利申请量以及相关数据.
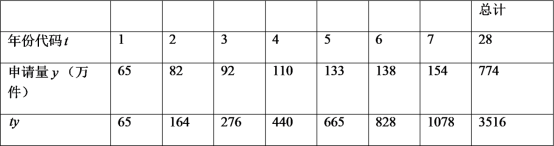
注:年份代码![]() ~
~![]() 分别表示
分别表示![]() ~
~![]() .
.
(1)可以看出申请量每年都在增加,请问这几年中哪一年的增长率达到最高,最高是多少?
(2)建立![]() 关于
关于![]() 的回归直线方程(精确到
的回归直线方程(精确到![]() ),并预测我国发明专利申请量突破
),并预测我国发明专利申请量突破![]() 万件的年份.
万件的年份.
参考公式:回归直线的斜率和截距的最小二乘法估计分别为 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】峰谷电是目前在城市居民当中开展的一种电价类别.它是将一天24小时划分成两个时间段,把8:00—22:00共14小时称为峰段,执行峰电价,即电价上调;22:00—次日8:00共10个小时称为谷段,执行谷电价,即电价下调.为了进一步了解民众对峰谷电价的使用情况,从某市一小区随机抽取了50 户住户进行夏季用电情况调查,各户月平均用电量以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:度)分组的频率分布直方图如下图:
(单位:度)分组的频率分布直方图如下图:

若将小区月平均用电量不低于700度的住户称为“大用户”,月平均用电量低于700度的住户称为“一般用户”.其中,使用峰谷电价的户数如下表:
月平均用电量(度) |
|
|
|
|
|
|
使用峰谷电价的户数 | 3 | 9 | 13 | 7 | 2 | 1 |
(1)估计所抽取的 50户的月均用电量的众数和平均数(同一组中的数据用该组区间的中点值作代表);
(2)(![]() )将“一般用户”和“大用户”的户数填入下面
)将“一般用户”和“大用户”的户数填入下面![]() 的列联表:
的列联表:
一般用户 | 大用户 | |
使用峰谷电价的用户 | ||
不使用峰谷电价的用户 |
(![]() )根据(
)根据(![]() )中的列联表,能否有
)中的列联表,能否有![]() 的把握认为 “用电量的高低”与“使用峰谷电价”有关?
的把握认为 “用电量的高低”与“使用峰谷电价”有关?
| 0.025 | 0.010 | 0.001 |
| 5.024 | 6.635 | 10.828 |
附:![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3![]() ,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<
,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<![]() ).则下列叙述错误的是( )
).则下列叙述错误的是( )
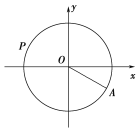
A.R=6,ω=![]() ,φ=-
,φ=-![]()
B.当t∈[35,55]时,点P到x轴的距离的最大值为6
C.当t∈[10,25]时,函数y=f(t)单调递减
D.当t=20时,|PA|=6![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+(1﹣2a)x﹣lnx(a∈R).
(1)讨论f(x)的单调性;
(2)当a>0时,证明f(x)≥ln(ae2)﹣2a(e为自然对数的底数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com