
①p:ab=0,q:a2+b2=0;?
②p:![]() q:
q:![]()
③p:x+y≠-2,条件q:x、y不都为-1.?
(2)已知p、q都是r的必要条件,s是r的充分条件,q是s的充分条件,那么?
①s是q的什么条件??
②r是q的什么条件??
③p是q的什么条件??
解:(1)①p![]() q(如a=0,b=1时,ab=0,而a2+b2=1≠0),又当a2+b2=0时,a=b=0,则ab=0,即q
q(如a=0,b=1时,ab=0,而a2+b2=1≠0),又当a2+b2=0时,a=b=0,则ab=0,即q![]() p.故p是q的必要不充分条件.?
p.故p是q的必要不充分条件.?
②由![]() 根据同向不等式可相加、相乘的性质有
根据同向不等式可相加、相乘的性质有![]() 即p
即p![]() q,但q
q,但q![]() p.?
p.?
反例:当α=1,β=5时,有![]() 而?α<2?.故p是q的充分不必要条件.?
而?α<2?.故p是q的充分不必要条件.?
③欲判断“p![]() q”,可转化为判断“
q”,可转化为判断“![]() q
q![]()
![]() p”,即判断命题:“若x、y都为-1,则x+y=-
p”,即判断命题:“若x、y都为-1,则x+y=-![]() q
q![]()
![]() p”是真命题.?
p”是真命题.?
又“若x+y=-2,则x、y都为-![]() p
p![]()
![]() q”.?
q”.?
由上可知,p是q的充分不必要条件.?
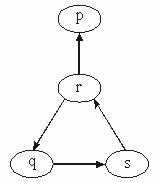
(2)先根据已知条件,用上图表示p、q、r、s之间的相互关系.?
由图可知:①q![]() s,s
s,s![]() r
r![]() q,?
q,?
s是q的充要条件.?
②因为r![]() q,q
q,q![]() s
s![]() r,?
r,?
所以r是q的充要条件.?
③因为q![]() s
s![]() r
r![]() p,?
p,?
所以p是q的必要条件.?
点评:判断p是q的什么条件,通常有如下两种方法:?
(1)定义法,即把题目中所给条件按逻辑关系画出箭头示意图,再用定义进行判断.?
通常对p![]() q要予以证明,p
q要予以证明,p![]() q可举反例说明.
q可举反例说明.
(2)转换法,即当所给命题的充分条件或必要条件不好判定时,可对命题进行等价转换,当p、q都很抽象时,可用“互为逆否的命题同时真或者同时假”来判定![]() p与
p与![]() q的关系.
q的关系.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源:全优设计选修数学-1-1苏教版 苏教版 题型:044
判定下列各题中,条件p是条件q的什么条件?(指明是充分不必要条件、必要不充分条件、充要条件或既不充分又不必要条件)
(1)p:ab=0,q:a2+b2=0;
(2)p:x=2,q:x2-7x+10=0;
(3)p:0<x<3;q:|x-1|<2;
(4)p:a+b-c=0,q:x=1是方程ax2+bx-c=0的根.
查看答案和解析>>
科目:高中数学 来源:设计选修数学-1-1苏教版 苏教版 题型:044
判定下列各题中,条件p是条件q的什么条件?(指明充分不必要条件、必要不充分条件、充要条件或既不充分又不必要条件)
(1)p:ab=0,q:a2+b2=0;
(2)p:x=2,q:x2-7x+10=0;
(3)p:0<x<3;q:|x-1|<2;
(4)p:a+b-c=0,q:x=1是方程ax2+bx-c=0的根.
查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com